Combien de temps dure un coucher de soleil ?

English introduction

Hey, that seems like a trivial question, but...

The obvious answer would seem to be :

The sun makes one revolution in 24 hours, i.e. 15° per hour, so it takes 4 minutes to cover 1°. The sun occupies about 1/2 a degree, so it takes 2 minutes to cover its "height". A sunset would therefore take about 2 minutes.

However, even the least knowledgeable of us know a few things that can put them off the scent:

• In the tropics, night falls very quickly. We can deduce from this that the sun dips below the horizon faster than at our latitudes, and must therefore cross the horizon more quickly.
• Beyond the Arctic Circle, we can see the midnight sun on certain days. There must therefore be one or more days when the sun shaves the horizon and continues to set.

Translated with www.DeepL.com/Translator (free version)

____________________________________________________________________

Tiens, voilà bien une question qui semble triviale. Et pourtant...

La réponse qui semble évidente à priori serait :

Le soleil fait un tour en 24h soit 15° par heure donc il lui faut 4 minutes pour parcourir 1°. Le soleil occupe environ 1/2 degré ; il lui faut donc 2 minutes pour parcourir sa ‘’hauteur’’. Un coucher de soleil durerait donc environ 2 minutes.

Toutefois, même les moins avertis savent, pour la plus part, des choses qui peuvent leur mettre la puce à l’oreille :

• Sous les tropiques, la nuit tombe très vite. On peut en déduire que le soleil plonge sous l’horizon plus vite que sous nos latitudes et donc qu’il doit franchir la limite plus rapidement.
• Au-delà du cercle polaire, on peut assister, certains jours, au soleil de minuit. Il doit donc y avoir un ou des jours où le soleil rase l’horizon et n’en fini pas de se coucher.

Alors reprenons avec en tête l’idée que la durée du coucher de soleil varie dans l’espace et dans le temps. On est obligé de faire des maths, même si quelques cas particuliers peuvent s’expliquer par le dessin.

Une bonne solution, pour analyser les choses compliquées, consiste à examiner les cas extrêmes, là où certains paramètres s’annulent ou sont égaux à 1.

A -À l’équateur

À l’équateur, les étoiles décrivent des cercles qui s’inscrivent dans des plans verticaux. (Si cela n’est pas évident pour vous, je vous invite à lire mon article « comment ça tourne »). Le soleil n’échappe pas à cette règle, simplement le plan concerné se décale de jour en jour au cours de l’année, du cercle rouge au vert de la figure 1et retour puis symétriquement coté nord.

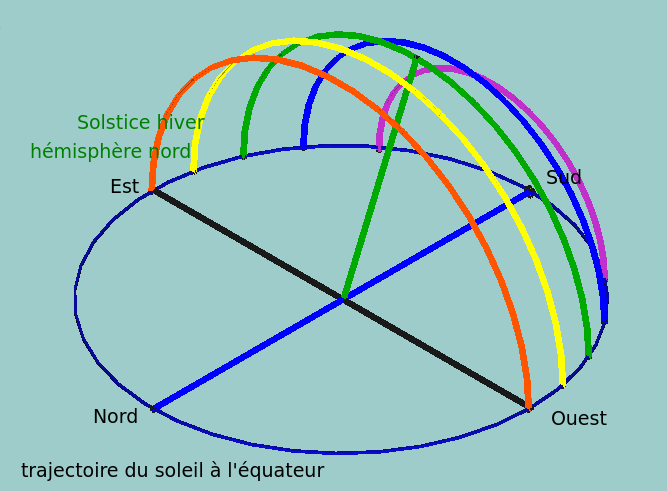
Figure 1

Notez que tous les arcs sont des demi-cercles, leurs centres sont au niveau du sol, sur la ligne bleue nord-sud qui est l'axe de rotation de la terre.( On triche un tout petit peu en le translatant au point d'observation).

A.I -Aux équinoxes

Aux équinoxes, partout sur terre, le soleil se lève exactement à l’est ¹ et se couche à l’ouest. Au coucher, à l’équateur, il plonge donc verticalement suivant le cercle rouge figure 1.

Dans cette situation, et seulement dans cette situation, le calcul présenté plus haut est tout à fait juste : À l'équateur, aux équinoxes, le coucher de soleil dure effectivement 2 minutes, seulement 2 jours par an. ².

A.II -Aux solstices

Au solstice d’hiver de l’hémisphère nord, le plan du cercle décrit s’est déplacé au sud. On est sur le cercle vert de la figure 1. La ligne droite verte est inclinée de 23,4° par rapport à la verticale ( l’inclinaison de l’axe de la terre par rapport au plan de l’écliptique). Le rayon du cercle vert est égal à celui du cercle rouge multiplié par cos(23,4°) Le cercle décrit étant plus petit, le soleil y occupe un plus grand espace relativement à la circonférence donc la durée du coucher va être supérieure à nos 2 minutes précédentes, en fait divisée par cos(23,5°) ce qui nous fait 2,18 minutes = 131s.

Au solstice d’été c’est la même chose mais symétriquement.

Ainsi à l’équateur la durée du coucher varie entre 120s et 131s.

A.III -Avec la trigonométrie sphérique

Si jusque là on a pu s’en passer, on n’y coupera pas tôt où tard. Bon, c’est plus pénible que compliqué : il suffit de remplacer les sinus et cosinus par leur valeurs.

La hauteur d’une étoile est donnée par la formule :

sin(h) = sin(L) x sin(D) + cos(L) x cos(D) x cos(H)

où h est la hauteur ; L la latitude du lieu d’observation ; D la déclinaison du soleil et H son angle horaire.

À l’équateur, L = 0 donc sin(L) = 0, ce qui simplifie la formule en :

sin(h) = cos(D) x cos(H)

donc cos(H) = sin(h) / cos(D)

A.III.a -À l’équinoxe

La déclinaison du soleil est nulle, cos(D) = 1, la formule se simplifie encore :

cos(H) = sin(h)

Donc H est le complément de h

Au début du coucher, h_D = 0,25°. H_D = 90° – 0,25° = 89,75°.

À mi-coucher (le centre du soleil est à raz de l’horizon) h_mc = 0 et H_mc = 90°

Le soleil parcourt 90 – 89,75 = 0,25° ce qui demande 1 min.

La durée du demi-coucher est de 1 min ; le coucher dure 2 minutes. C’est bien ce qu’on avait vu plus haut.

A.III.b -Aux solstices

La déclinaison du soleil est de ± 23,4°. On a sin(23,4°) = 0,397148 et cos(23,4°) = 0,917754

sin(h) = cos(23,4) x cos(H)

cos(H) = sin(h) / cos(23,4°)

Au début du coucher, h_D = 0,25° ; sin(h_D) = 0,004363

cos(H_D) = 0,004363 / 0,917754 = 0,004754

H_D = arccos(0,004754) = 89,727°

À mi-coucher h_mc = 0 donc sin(h_mc) = 0 donc cos(H)= 0 donc H_mc = 90°

Le soleil parcourt 90 – 89,727 = 0,273° ce qui demande

0,273 x 4 = 1,092 min .

Le coucher dure 2 x 1,092 min = 2,184 min = 131s.

B -Aux pôles

Aux pôles, le parcours du soleil au cours de l’année ressemble au filetage d’une vis. En première approximation, sur une journée, le soleil décrit un cercle dans un plan horizontal.

B.I -Au solstice d’hiver

Le soleil est sous l’horizon : pas de coucher, ou plutôt le coucher est permanent.

B.II -Au solstice d’été

Le soleil trône à 23,4° de hauteur toute la journée. Pas de coucher

B.III -Aux équinoxes

Partout sur terre on a un demi ensoleillement : 12h de soleil, 12 h sans soleil. Aux pôles on a aussi un demi ensoleillement sous la forme de 24 h de demi soleil : Le centre du soleil est à raz de l’horizon toute la journée. On est donc en situation de demi-coucher.

Seul l’équinoxe d’automne correspond à un coucher. L’autre correspond à un lever de soleil.

Reprenons notre équation :

sin(h) = sin(L) x sin(D) + cos(L) x cos(D) x cos(H)

On a L = 90° donc sin(L)= 1 et cos(L) = 0 le deuxième terme de l’addition ci-dessus disparaît.

L’équation devient

sin(h) = sin(D) donc h = D.

La hauteur ne dépend que de la déclinaison. Celle-ci varie sinusoïdalement sur une période de 365,25 jours, avec une amplitude de 23,4°. À la fin du demi-lever h_mc = 0,25° ce qui représente 0,25 / 23,44 = 0,0107 fois l’amplitude de déclinaison. On a arcsin(0,0107) = 0,6111° donc la hauteur h_mc = 0,25° est atteinte quand on a parcouru 0,6111° sur la sinusoïde d’une période de 365,25 jours soit une durée de 365,25 / 360 x 0,6111 = 0,620 jour soit approximativement 14,9 h. Aux pôles, le lever complet à l’équinoxe de printemps dure 2 x 14,88 heures = 29,76 h et c’est la même chose pour le coucher à l’équinoxe d’automne.

C -Au cap Moriss Jesup

C’est le point le plus au nord du Groenland. Latitude environ 83°.

Reprenons notre équation :

sin(h) = sin(L) x sin(D) + cos(L) x cos(D) x cos(H)

On a sin(L) = 0,99255  ; cos(L) = 0,12187 

C.I -Aux équinoxes

D = 0 donc sin(D) = 0 et cos(D)=1 

l’équation devient :

sin(h) = cos(L) x cos(H)

sin(h) = 0,12187 x cos(H)

cos(H) = sin(h) / 0,12187

Au début du coucher, h_D = 0,25° ; sin(h_D) = 0,004363

cos(H_D) = 0,004363 / 0,12187 = 0,0358

H_D = arccos(0,0358) = 87,948°

À mi coucher sin(h_mc) = 0 donc cos(H_mc)=0 ; H_mc = 90°

Pendant le demi-coucher, le soleil parcourt 90° - 87,948° = 2,051° ce qui prend 8,207 min.

Au cap Moriss, aux équinoxes, le coucher dure 16,414 min, plus d’un quart d’heure ! = 985s

C.II -Aux solstices

Le soleil tourne dans un plan incliné de 7° par rapport au sol. Insuffisant pour avoir un coucher ou un lever. Vérifions :

sin(h) = sin(L) x sin(D) + cos(L) x cos(D) x cos(H)

cos(23,4°)= 0,917754 ; sin(23,4°)= 0,397148 ; sin(L) = 0,99255 et cos(L) = 0,12187

À midi solaire cos(H₁₂) = 1 donc sin(h)= sin(L) x sin(D) + cos(L) x cos(D)

sin(h₁₂) = 0,99255 x 0,39714 + 0,12187 x 0,9177

sin(h₁₂) = 0,506021

h₁₂ = arcsin(0,506021) = h₁₂=30,4°

À minuit cos(H₀) = -1

sin(h₀) = 0,99255 x 0,39714 - 0,12187 x 0,9177

sin(h₀) = 0,28234121

h₀= 16,4°

Au cap Moriss, au solstice d'été, le soleil oscille entre 16,4° et 30,4°. Ni lever, ni coucher.

D -En France à 45° de latitude

Cette latitude est relativement centrale en France et bien commode car sin(L) = cos(L) = 1 / √2 = 0,707 (ce qui est précis à 1,5/10000).

La figure 2 montre les trajectoires des étoiles et du soleil  sous 45° de latitude coté sud.

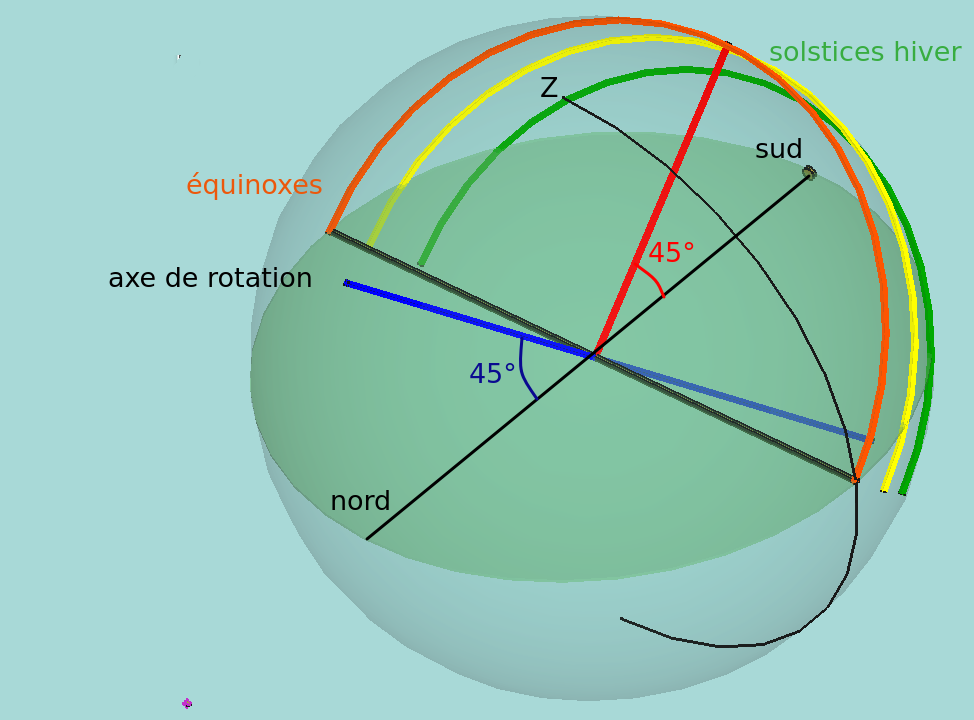
Figure 2

Ici, seul le demi-cercle rouge a son centre au niveau du sol. Les centres des arcs jaune et vert sont enfoncés dans le sol. Ils sont sur l'axe de rotation de la terre qui est incliné de 90° par rapport à la ligne droite rouge ( On triche un tout petit peu en le translatant au point d'observation).. Ainsi on en voit moins d'un demi-cercle.Le coucher à lieu avant H = 90°.

Pour les arcs symétriques, coté nord (non représentés), c'est le contraire. Leurs centres sont au-dessus du sol et donc on en voit plus de la moitié..Le coucher à lieu au-delà de  H = 90°.

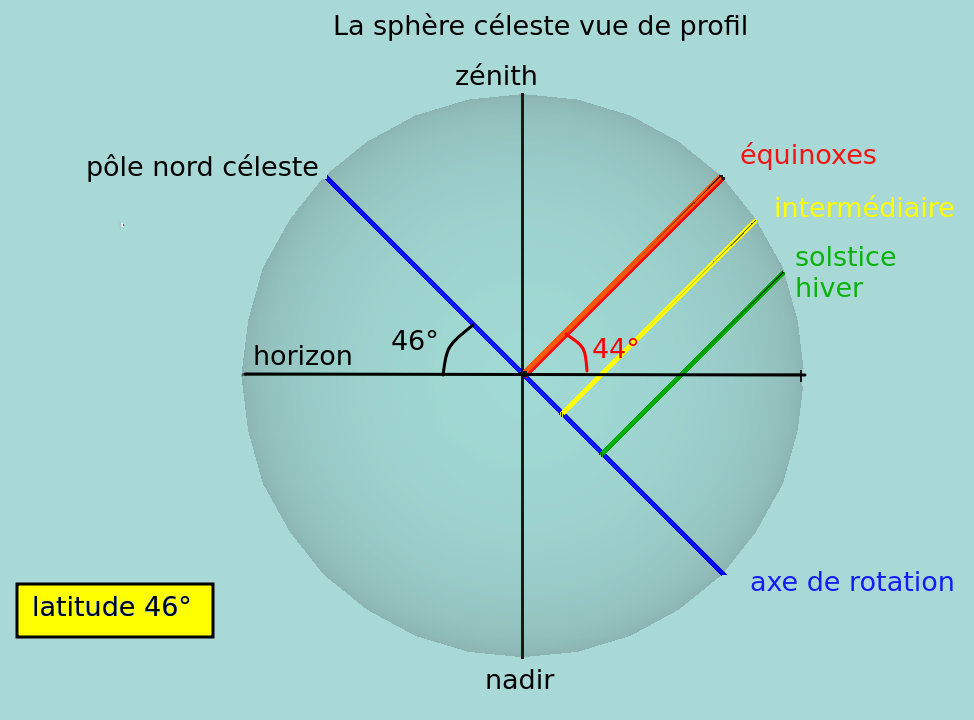
Figure 3

On a :

sin(h) = 0,707 x sin(D) + 0,707 x cos(D) x cos(H)

sin(h) – 0,707 x sin(D) = 0,707 x cos(D) x cos(H)

cos(H) = (sin(h) – (0,707 x sin(D)) / (0,707 x cos(D))

D.I -Aux équinoxes

À mi-coucher H_mc=90° (horizon ouest).

D = 0 donc sin(D) = 0 et cos(D) = 1 ce qui nous donne :

cos(H) = sin(h) / 0,707 = sin(h) x √2

et comme h est très petit :

cos(H) = h x √2 (h en radians)

Au début du coucher, h= 0,004363 rd

cos(H_D ) = 0,004363 x √2 =0,06170

H_D = arccos(0,006170) = 89,646°

À mi-coucher H_mc=90° (horizon ouest, demi-cercle rouge de la figure 2))

Le demi-coucher s’étend sur 90 – 89,646 = 0,3536°

Il dure 0,3536 * 4 = 1,414 min*

Sous 45° de latitude, aux équinoxes, le coucher dure √2 fois plus longtemps qu’à l’équateur soit 2,83min = 170s.

Ceci peut se comprendre en reconsidérant la figure 2. Le cercle rouge est incliné de 45° ; pour s’élever de h° il faut parcourir h x √2° sur le cercle.

(l'hypoténuse d'un triangle rectangle isocèle mesure √2 fois les cotés de l'angle droit). On peut généraliser facilement : Aux équinoxes, le coucher dure 2 min / cos(L) .

D.II -Au solstice d’été

La déclinaison du soleil est de 23,4° ; sin(D)= 0,39715 et cos(D)= 0,91775.³

Au début du coucher, sin(h_D) = 0,004363

­rappel cos(H_D) = (sin(h_D) – 0,707 x sin(D)) / 0,707 x cos(D)

En séparant les 2 termes de la soustraction :

cos(H_D) = ( sin(h_D) x √2 / cos(D) ) – (sin(D) / cos(D))

cos(H_D) = 0,00672320 – 0,432743

cos(H_D) = -0,42602

H_D = arccos(-0,42602) = 115,21°

À mi-coucher, le premier terme de la soustraction disparaît

cos(H₀) = -0,432743

H₀= arccos(-0,432743) = 115,64°

Le demi-coucher s’étend sur 115,64 – 115,21 = 0,43° ce qui correspond à 1,72min

Sous 45° de latitude, au solstice d'été, le coucher dure 3,440 min = 206 s .

D.III -Au solstice d’hiver

La déclinaison du soleil est de -23,4° ; seul sin(D) change (de signe) = -0,39715.

Au début du coucher, La soustraction précédente devient une addition en prenant la valeur absolue de sin(D).

cos(H_D) = ( sin(h_D) x √2 / cos(D) ) + (sin(D) / cos(D))

cos(H_D) = 0,00672320 + 0,432743

Comme le premier terme est très petit en valeur absolue par rapport au second, la valeur de la somme est pratiquement identique (au signe près) à celle de la soustraction du solstice d’été.

cos(H_D) = 0,439466

H_D= arccos(0,439466) = 63,93°

À mi-coucher, cos(H₀) = 0,28079 / 0,64885 = 0,43275

H₀= arccos(0,43275) = 64,36°

Le demi-coucher s’étend sur 64,36 – 63,93 = 0,43° ce qui correspond à 1,72min

Sous 45° de latitude, au solsticee d'hiver, le coucher dure 3,44 min = 206s

E -Avec Stellarium

Avec Stellarium, vous pouvez déterminer la durée d’un coucher de soleil d’un jour quelconque sous une latitude quelconque.

En cliquant sur la première icône dans la barre d’outil à gauche, vous pouvez choisir une latitude. Cliquez ensuite sur la croix de la fenêtre concernée, vous n’en avez plus besoin.

Avec la loupe (4^e icône ou F3), demandez à voir le soleil. Vous devriez avoir les données concernant le soleil en haut à gauche, en particulier son azimut et sa hauteur. Si ce n’est pas le cas, voyez l’icône clé à fourche (ou F2), onglet informations.

Affichez la fenêtre des heures 2^e icône à gauche ou F5.

Bloquez le défilement du temps : Ça se passe dans la barre d’outils du bas ; voyez l’icône ▶ qui devient ▍▍.

Choisissez la date dans la fenêtre « date et heure ».

Faites défiler les heures, puis les minutes puis les secondes en contrôlant la hauteur du soleil. Arrêtez vous au plus près de 0,25°. Notez l’heure, les minutes et les secondes.

Faites défiler quelques minutes puis les secondes. Arrêtez vous au plus près de 0°. Notez l’heure, les minutes et les secondes.

Calculez l’écart de temps en secondes entre les deux relevés.

Exemple : 21h 18’ 22’’ et 21h 20’ 31’’

Il n’y a pas de changement des heures.

Pour aller à 19’ 0’’ il faut ajouter 60 – 22 = 38s .

Pour aller à 20’ il faut ajouter 1 minute soit 60s.

Au total la durée est de 38 + 60 + 31 = 129s.

Vous pouvez aussi calculer : 21h 18’ 21’’ = 21 x 3600 + 18 x 60 + 22 = 76702

et 21h 20’ 31’’ = 21 x 3600 + 20*60 + 31 = 76831

La différence est 76831 – 76702 = 129s

Notez que vous pourriez ici vous dispenser de 21 x 3600.

E -Conclusion

Nous voici au terme de ce questionnement apparemment anodin, mais qui nous a permis d’approfondir un certain nombre de choses.

Pour terminer, je vous propose un tableur Calc qui permet de faire instantanément les calculs pour une latitude quelconque hormis les cas farfelus trop proche des pôles. Seule la cellule de la latitude est modifiable par l'utilisateur.

 __________________________________________________________________________________________________________________________________________________

1 Stricto sensu, l’équinoxe ne dure qu’un instant. Au moment du coucher on n’ est donc plus tout à fait à l’équinoxe. On fait donc ici une légère approximation.

2 Autre approximation : La taille du soleil n’est pas exactement de 30’ et d’ailleurs elle varie au cours de l’année.

3 Je prend beaucoup de décimales à cause de la soustraction plus loin qui doit laisser suffisamment de chiffres significatifs