Si la lune était une boule parfaite

Jusqu’à l’époque de Galilée, on affirmait qu’il existait deux mondes. Le bas monde, dit monde sublunaire, imparfait et le monde céleste, domaine de la perfection divine. Dans ces conditions, la lune devait être une sphère parfaite, rigoureusement lisse.

Galilée disait à ses contemporains : « Si la lune était une sphère parfaite, vous ne la verriez pas ». Par pure curiosité, je vous propose de voir jusqu’à quel point il avait raison.

Until the time of Galileo, it was asserted that there were two worlds. The lower world, called the sublunary world, imperfect and the celestial world, the domain of divine perfection. Under these conditions, the moon had to be a perfect sphere, rigorously smooth.

Galileo said to his contemporaries: "If the moon were a perfect sphere, you would not see it. Out of pure curiosity, I suggest you see how right he was. 

Translated with www.DeepL.com/Translator (free version)

A -Un peu d’optique

Pour les moins aguerris, j’explique ici les bases des lois de la réflexion en optique.

Examinons la figure ci-dessous.

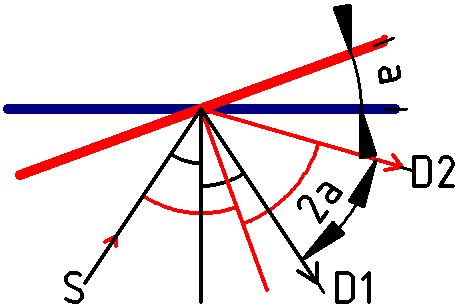
Le gros trait bleu représente un miroir. Le gros trait rouge montre le même miroir tourné d’un angle a.

La lumière provient d’une source S. En position bleue, le faisceau, après réflexion, prend la direction D1. Les angles repérés en noir sont égaux (angle d’incidence = angle de réflexion).

En position rouge, le faisceau, après réflexion, prend la direction D2. Les angles repérés en rouge sont égaux.

L’angle entre les directions D1 et D2 vaut 2a.

Examinons la figure suivante

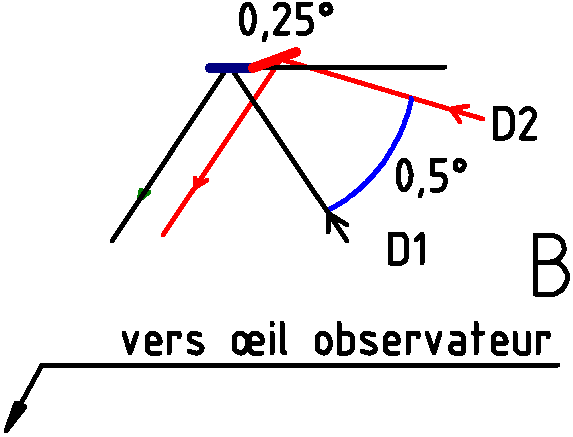
Nous avons un miroir avec deux facettes présentant un angle de 1/4° entre elles.

Le faisceau D1 provient d’un point au bord du soleil. Le faisceau D2 provient du point diamétralement opposé. L'angle entre les 2 directions est celui sous lequel on voit le soleil soit environ 0,5°.

Les 2 faisceaux convergent sur l’œil de l’observateur.

B -La lune en bille parfaite

Supposons la lune comme une sphère parfaite sans la moindre aspérité même microscopique. Elle aurait alors l’aspect d’une énorme bille de roulement. Une telle sphère peut être considérée comme un ensemble de facettes en nombre infini. Les considérations ci-dessus nous permettent de comprendre que quand le soleil éclaire une bille parfaite, l’ensemble des facettes couvrant un angle de 0,25° renvoie sa lumière dans une même direction qui peut être l’œil de l’observateur.

Ainsi, si la lune était plus lisse  que le crane d’un chauve, chaque observateur n’en verrait qu’un disque couvrant 0,25° de sa périphérie.

NB: Ce calcul est le même que celui qui permet d'évaluer la taille d'une étoile artificielle obtenue en faisant briller une petite bille sous le soleil.

Dès lors le calcul est très simple.

La lune a une circonférence d’environ 10 000km (on se contente ici d’un calcul à la louche).

Un cône de 0,25° dont le sommet est au centre de la lune  à une base de diamètre 10 000 / 360 / 4 ≅ 7km à la surface de la lune.

La lune est en moyenne à 384 000 km de la terre, donc un cercle de 7km est vu sous un angle de 7 / 384 000 = 1,‚82 x 10^-5 rd soit 0,001°

Le point brillant de la lune serait vu sous 0,001° soit 0,06’ alors que la résolution de l’œil humain est de l’ordre de 1’!

La lune serait vue comme une étoile. 

C -Quelle magnitude pour cette ‘’étoile’’ ?

À supposer que la lune soit parfaite, son coefficient de réflexion serait de 100 % et son coefficient de diffusion nul.

Considérons les rayons issus du centre du soleil et qui seront réfléchis vers nous. Ils couvrent sur la bille un angle de 0,25°. Après réflexion sur la petite zone concernée, ils forment un cône de 0,5° d’angle au sommet .

Les points à la périphérie du soleil forment eux, une infinité de cônes de 0,5° mais dont les axes sont inclinés de 0,25° dans toutes les directions.

L’ensemble constitue un cône de 0,5 + 2 x 0,25 = 1° d’angle au sommet.

La lune est à environ 384000km. Je néglige le fait que le point focal est un demi rayon de lune au-delà. Au niveau de la terre, on a une tache circulaire dont le diamètre est de 384000 x tg(1°) = 6700km. Le rapport entre l’éclairement sur la bille (la zone brillante de 7km de diamètre) et celui au sol est égal au rapport des aires donc au carré de 6700 / 7 soit 916 000 en arrondissant.

Notre étoile serait 916 000 fois moins lumineuse que le soleil. Arrondissons à 1 million, on ne recherche pas la précision ici, juste un ordre de grandeur.

5 magnitudes correspondent plus ou moins à un facteur 100. Un facteur 1 million correspond donc à 15 magnitudes.

La magnitude du soleil est d’environ -27. On chute de 15 magnitudes il reste :

-27 + 15 = -12.

La lune serait vue comme une étoile de magnitude -12 donc monstrueusement brillante.

Rappelons que la magnitude de Vénus, dans ses meilleurs jours, ne dépasse pas -4,6.

Ce calcul contient des approximations, il ne prétend pas fournir autre chose qu’un ordre de grandeur. En particulier la grosse tache circulaire n’est pas uniformément lumineuse.

D’autre part, on a supposé que le soleil frappait la lune suivant la normale de la zone réfléchissante. C’est plus ou moins ce qui se passe à la pleine lune, mais à la nouvelle lune le point réfléchissant vers nous est déplacé vers un bord et  frappé en incidence rasante, la luminosité est multipliée par un cosinus proche de 0. Ainsi verrait-on notre ‘’étoile’’ varier en magnitude durant une lunaison et d’autre part son mouvement serait celui que nous attribuons au satellite, modulé par une ondulation suivant un diamètre en phase avec sa modulation en luminosité.

L’humanité aurait-elle envisagé de se poser sur ce drôle de petit astre de 7km de diamètre ? Certainement pas dans un premier temps, mais quelle surprise en essayant d’en faire le tour avec une sonde exploratrice aveugle puisqu'aucune lumière ne serait diffusée par la surface!

Addendum:

Un ancien professeur de physique de l'université de Besançon m'a fait remarquer que l'on aurait pu s'apercevoir de la présence d'un gros objet par l'occultation des étoiles "passant" derrière et par les éclipses totales de soleil. Les éclipses de lune se traduiraient par une disparition temporaire de la fausse étoile.

***** © M Guignard 2021 *****