Le système des coordonnées équatoriales

Dans ce qui suit, on raisonne sur la sphère céleste, c'est à dire sur le ciel tel qu'il nous apparaît : une immense sphère creuse dont la Terre serait le centre et qui tournerait sur elle même autour d'un axe passant par les pôles terrestres.
Pour repérer un point sur une sphère on utilise deux angles. Par exemple un lieu terrestre est défini par sa longitude et sa latitude.

A -Les coordonnées terrestres

Les points de même longitude sont sur un demi grand cercle allant du pôle nord au pôle sud et coupant l'équateur à angle droit. Ce demi grand cercle est appelé un méridien parce qu'à midi solaire, donc au milieu de la journée, le Soleil est exactement au dessus du méridien du lieu d'observation. Le midi solaire à lieu au même moment pour toutes les personnes habitant sur un même méridien, donc pour les lieux de même longitude. Les méridiens issus d'un pôle font penser aux baleines d'un parapluie attachées au sommet de celui-ci. Nous reprendrons cette image plus loin.
Le méridien passant par Greenwich, donne par convention la longitude 0. L'équateur est doublement gradué comme un rapporteur à partir de là, en partant vers l'est et vers l'ouest. La graduation 180° est commune au deux ensembles de graduations.
Les points de même latitude sont sur un cercle plus ou moins grand, toujours parallèle à l'équateur et dont le centre est sur l'axe de rotation de la Terre. Ces cercles sont appelés des parallèles (au masculin). Tout ceux qui habitent sur un même parallèle, voient le Soleil et les étoiles effectuer sensiblement un même parcours un jour donné. Si on néglige le mouvement de la Terre autour du Soleil, on peut dire qu'un point donné de la Terre décrit son propre parallèle  en une journée. Pour trouver la latitude d'un point, il suffit de graduer son méridien en partant de l'équateur.
Remarquons enfin qu'on aurait pût placer le point d'attache des baleines de parapluie ailleurs qu'aux pôles. Chaque point de la Terre aurait été parfaitement défini par ses deux coordonnées mais les points d'une même baleine n'auraient pas présenté une caractéristique commune comme le font les méridiens ; de même pour les parallèles.

B - Les coordonnées célestes

Pour définir la position d'une étoile, on peut se repérer par rapport à la Terre. Les deux angles sont alors l'azimut et la hauteur, les coordonnées sont dites azimutales ou altazimutales.

 ♦ L'azimut est l'angle entre la direction sud et celle de l'étoile. Les angles sont comptés dans le sens horaire : L'ouest est à 90°, l'est à 270° et une étoile qui serait 1° plus à l'est que le sud aurait un azimut de 359°.

♦ La hauteur est l'angle entre l'horizontale à l'azimut de l'étoile et la ligne qui va de notre œil à l'étoile.
Bien qu'il paraisse naturel, ce système n'est pas idéal car les coordonnées d'une étoile ainsi définies varient avec l'heure, la date et le lieu d'observation. Impossible dans ces conditions d'établir des cartes universelles. Pour s'en convaincre, il suffit de se demander à quel point du ciel sont attachées les baleines de parapluie : au zénith de chaque lieu d'observation. C'est pourquoi les astronomes utilisent un autre système : Les coordonnées équatoriales, où les points de repère sont fixés au ciel et non à la Terre.
Le système est calqué sur les coordonnées terrestres avec deux pôles et un équateur. Le pôle nord terrestre est remplacé par le pôle nord céleste : l'endroit ou l'axe de rotation de la Terre vient ‘crever’ la sphère céleste, matérialisé approximativement par l'étoile polaire. Le pôle sud céleste est l'équivalent coté sud.  L'équateur céleste est dans le même plan que l'équateur terrestre. Si on imagine un grand fil à couper le beurre attaché au centre de la Terre et tendu jusqu'au delà de la sphère céleste et qu'on le fait tourner de façon à couper la Terre en deux suivant l'équateur terrestre, il coupera la sphère céleste en deux suivant l'équateur céleste. Remarquons que les points d'attache des baleines de parapluie correspondent au zénith des observateurs des  pôles ; pour eux les coordonnées azimutales et équatoriales sont confondues.
Les longitudes terrestres sont devenues des ascensions droites (AD ou α, RA = right ascension en anglais) et les latitudes des déclinaisons (D ou δ). Toutefois les AD sont graduées non pas en angles mais en heures de 0 à 24h.
Le point 0,0 est celui où le Soleil se trouve à l'équinoxe de printemps lorsque sa trajectoire apparente coupe l'équateur céleste. On l'appelle le point vernal. Il est situé actuellement dans la constellation des Poissons.
L'ascension droite au méridien correspond à l'heure sidérale du lieu et du moment d'observation. Ainsi en descendant vers l'est on trouve des AD de plus en plus grandes puisqu'elles atteindront le méridien de plus en plus tard. C'est  l'inverse vers l'ouest.
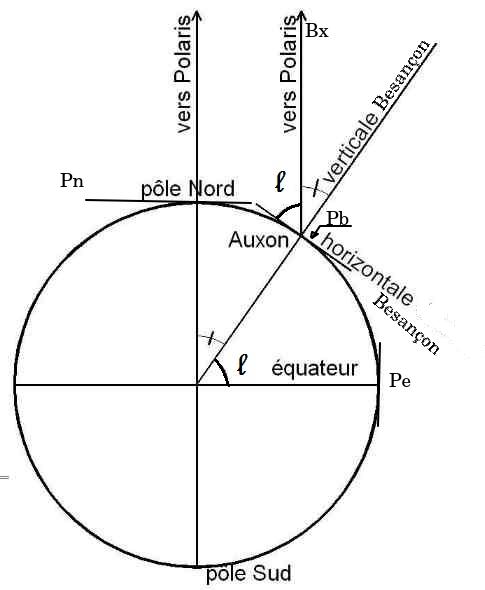
Le ciel tourne donc autour d'un axe passant par  l'étoile polaire et l’œil de l'observateur assimilable au centre de la Terre. Cet axe est incliné par rapport au sol de la latitude du lieu. De même que chaque point terrestre décrit un parallèle, chaque étoile décrit un cercle centré sur cet axe. Tous ces cercles sont parallèles entre eux et inclinés du complément à la latitude du lieu. L'équateur passe par les horizons est et ouest et au sud il est à une hauteur égale au complément de la latitude.

Ce système de coordonnées présente un grand avantage : Si la monture du télescope possède un axe orienté suivant celui de la sphère céleste, cet axe pourra être gradué en ascensions droites, tandis qu'un autre axe, perpendiculaire au premier, sera gradué en déclinaisons. De plus le mouvement de rotation de la sphère céleste sera compensé en faisant uniquement tourner l'axe d'ascension droite dit aussi axe polaire. On pourra donc maintenir facilement un objet céleste dans le champ d'observation. L'opération peut être automatisée en utilisant un moteur tournant à la vitesse exacte nécessaire ce qui autorise la photo à longue pause. Une telle monture existe et s'appelle monture équatoriale. Elle comporte quatre axes de rotation. Les deux premiers servent uniquement à orienter correctement l'axe polaire. Cette opération est appelée la mise en station.

Pour trouver une étoile il suffit d'afficher ses coordonnées équatoriales. Notons cependant que du fait de la rotation de la sphère céleste, le repère de lecture des AD doit être ajusté au préalable et retouché constamment.
Les montures plus simples, dites montures azimutales ou altazimutales, sont tout de même utilisées assez souvent car elles sont moins chères. Il existe des équations permettant de passer d'un système de coordonnées à l'autre. Ainsi on peut pointer un objet avec ses coordonnées azimutales du moment et du lieu, après avoir fait calculer celles-ci par un petit programme tournant sur une calculette de type lycée, ou par un logiciel d'astronomie tournant sur un ordinateur portable. Avec ce type de monture, le suivit peut être obtenu automatiquement en plaçant sous celle-ci un appareil appelé table équatoriale. Notons toutefois que la photo à longue pause bute sur un autre problème : la rotation du champ.

C- Le coin des matheux

À titre de curiosité, voici les équations qui permettent de passer des coordonnées équatoriales aux coordonnées azimutales :

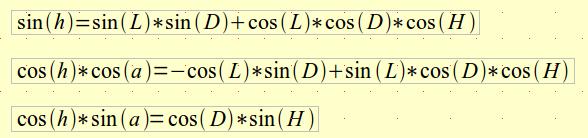
où h = hauteur ; a = azimut ; D = déclinaison ; H = angle horaire (0 au méridien) ; L = latitude

Au pôle, L = 90° d'où sin(L) = 1 et cos(L) = 0.
Dans ces conditions la première équation se simplifie et devient : sin(h) = sin(D).  Donc h = D. En clair, la hauteur d'une étoile est constante et égale à sa déclinaison. C'est ce que laissait prévoir la phrase ci-dessus : Pour un observateur aux pôles, les coordonnées équatoriales et azimutales sont confondues.

***** © M Guignard ****