jusqu’où voit-on au bord de la mer
A -distance de la ligne d’horizon
La distance de la ligne d’horizon, lorsqu’on est au bord de la mer est limité par la rotondité de la terre. Cette distance varie avec l’altitude des yeux de l’observateur. Voyons cela de plus près et essayons de calculer cette distance en utilisant la figure ci-dessous .
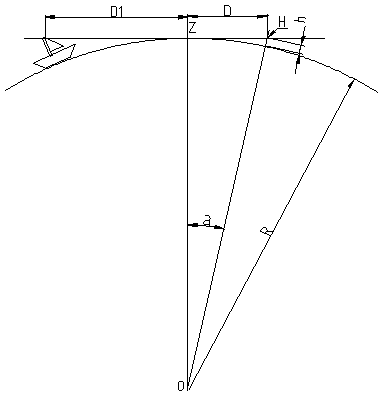
Figure 1
R est le rayon de la terre ; h représente la hauteur des yeux au-dessus de la mer.
Le regard porte jusqu’au point de tangence avec la mer (point Z) ; D est la distance entre l’observateur et le point de l’horizon Z.
A.I -Approche avec un cas particulier
Dans un premier temps, on va supposer que les yeux de l’observateur sont à 1m au-dessus du niveau de la mer (il a les pieds dans l’eau).
La distance OH est égale au rayon terrestre R plus 1m.
cos(a) = R / (R + 1)
R vaut environ 6400km soit 6 400.000m
cos(a) = 6 400 000 / 6 400 001 = 0,999 999 843 750
et a = acos(0,999 999 843 750) = 0,000 559 rd
On a tg(a) = D / R donc D = tg(a) x R
Comme a est très petit, sa tangente est égale à a en rd.
D= 0,000 577 559 * 6 400 000 = 3696m soit environ 3,7km.
A.II -Comment varie D en fonction de h
Le calcul précédent est un peu lourd. Il ne donne pas une vision synthétique de la façon dont D s’accroît quand h augmente. Alors, reprenons sous un autre angle.
Considérons le triangle rectangle Z0H de la figure 1.
Le théorème de Pythagore nous dit que D2 + R2 = OH2.
Donc D2 = OH2 – R2
Comme OH = R + h , on a OH2 = R2 + 2Rh + h2.
Donc D2 = 2Rh + h2.
Le terme h2 étant négligeable devant 2Rh, on écrira D = √2Rh. Le terme 2R étant constant, on voit que D varie comme √h.
Ainsi pour une altitude donnée en mètres, il suffira de multiplier la racine de cette hauteur par 3700m pour obtenir D avec une légère approximation.
Plus précisément, D = √2Rh + h2 = √h x √2R + h .
Comme 2R = 12 800 000m, on voit bien que D = √2Rh est une excellente approximation le terme h reste négligeable même si on prend l’avion et qu’on monte à 10 000m.
B -À partir de quelle distance aperçoit-on un navire en approche ?
La figure 1 répond à la question. La distance est la somme de D1 + D où D1 est la distance pour un objet de hauteur h1 et D la distance pour une altitude d’observation h.
Par exemple, pour un voilier avec une hauteur totale hors d’eau de 25m, D1 = 3700 x 5 m≈ 18,5km. Pour un observateur avec les yeux à 4m de hauteur, D = 3700 x 2 ≈ 7,4 km.
Le voilier serait donc visible (du moins le haut du mat) à 18,5 + 7,4 ≈ 26km. Mais la résolution de l’œil serait insuffisante même pour voir une voile carrée de 4m de large (visible cependant aux jumelles).1
Reprenons avec le Queen Mary dont j’estime la hauteur à 60m au-dessus de la ligne de flottaison et la largeur à 60m. D1 = 3,7km * √60 = 28,7km. Si on prend D =7,4km comme dans le calcul précédent cela nous fait une distance de 36km. L’angle sous lequel on voit le bateau est de 5,7’ pour 60m de largeur, donc on le verrait mais tout juste à l’œil nu (à condition de savoir où le chercher) mais nettement aux jumelles .
C -Pourquoi ne perçoit-on pas la courbure de la terre ?
Comme l’angle a est toujours petit, on peut dire qu’il est proportionnel à la racine carrée de h. On a vu que pour h = 1, il vaut 0,000 577 350rd ce qui nous fait environ 0,033°, ce qui correspond à la circonférence C divisée par 360 / 0,033 = 10909.
Pour une altitude de 100m, la portion de cercle devient 10 fois supérieure soit C / 1091.
Je vous invite, si l’occasion se présente, à prendre une ficelle de 5m et, sur une plage de sable, à tracer un arc de cercle en tendant la ficelle. La circonférence C = 10 x π = 31,4m et la longueur de l’arc qui nous intéresse est à peu près de 29mm. Pouvez vous faire la différence entre l’arc et sa corde ? Avis aux platistes ! Mais je doute qu’il en passe par ici.
D - Remarque :
Tout ceci est calculé en supposant un air absent ou parfaitement homogène. Dans la réalité, l'effet de la réfraction peut modifier sensiblement les valeurs théoriques. C'est ainsi que certains jours (très rares) on peut voir la Corse depuis la côte d'Azur!
Mes calculs restent valable dans les cas courants, avec de faibles hauteurs.
***** © M Guignard 2024 *****
1) À 24km de distance, une voile de 4m est vue sous un angle de 4/24000 = 0,000167rd soit 0,00095° ou 0,57’. On estime la résolution de l’oeil humain à 1’.

Comments powered by CComment