A -À l’équateur

À l’équateur, les étoiles décrivent des cercles qui s’inscrivent dans des plans verticaux. (Si cela n’est pas évident pour vous, je vous invite à lire mon article « comment ça tourne »). Le soleil n’échappe pas à cette règle, simplement le plan concerné se décale de jour en jour au cours de l’année, du cercle rouge au vert de la figure 1et retour puis symétriquement coté nord.

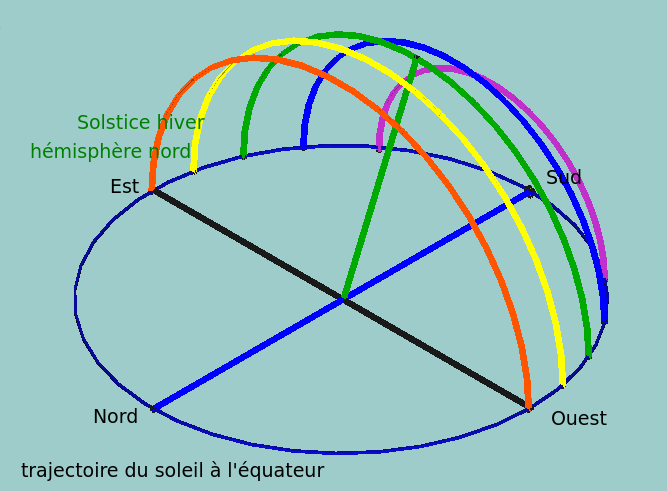
Figure 1

Notez que tous les arcs sont des demi-cercles, leurs centres sont au niveau du sol, sur la ligne bleue nord-sud qui est l'axe de rotation de la terre.( On triche un tout petit peu en le translatant au point d'observation).

A.I -Aux équinoxes

Aux équinoxes, partout sur terre, le soleil se lève exactement à l’est ¹ et se couche à l’ouest. Au coucher, à l’équateur, il plonge donc verticalement suivant le cercle rouge figure 1.

Dans cette situation, et seulement dans cette situation, le calcul présenté plus haut est tout à fait juste : À l'équateur, aux équinoxes, le coucher de soleil dure effectivement 2 minutes, seulement 2 jours par an. ².

A.II -Aux solstices

Au solstice d’hiver de l’hémisphère nord, le plan du cercle décrit s’est déplacé au sud. On est sur le cercle vert de la figure 1. La ligne droite verte est inclinée de 23,4° par rapport à la verticale ( l’inclinaison de l’axe de la terre par rapport au plan de l’écliptique). Le rayon du cercle vert est égal à celui du cercle rouge multiplié par cos(23,4°) Le cercle décrit étant plus petit, le soleil y occupe un plus grand espace relativement à la circonférence donc la durée du coucher va être supérieure à nos 2 minutes précédentes, en fait divisée par cos(23,5°) ce qui nous fait 2,18 minutes = 131s.

Au solstice d’été c’est la même chose mais symétriquement.

Ainsi à l’équateur la durée du coucher varie entre 120s et 131s.

A.III -Avec la trigonométrie sphérique

Si jusque là on a pu s’en passer, on n’y coupera pas tôt où tard. Bon, c’est plus pénible que compliqué : il suffit de remplacer les sinus et cosinus par leur valeurs.

La hauteur d’une étoile est donnée par la formule :

sin(h) = sin(L) x sin(D) + cos(L) x cos(D) x cos(H)

où h est la hauteur ; L la latitude du lieu d’observation ; D la déclinaison du soleil et H son angle horaire.

À l’équateur, L = 0 donc sin(L) = 0, ce qui simplifie la formule en :

sin(h) = cos(D) x cos(H)

donc cos(H) = sin(h) / cos(D)

A.III.a -À l’équinoxe

La déclinaison du soleil est nulle, cos(D) = 1, la formule se simplifie encore :

cos(H) = sin(h)

Donc H est le complément de h

Au début du coucher, h_D = 0,25°. H_D = 90° – 0,25° = 89,75°.

À mi-coucher (le centre du soleil est à raz de l’horizon) h_mc = 0 et H_mc = 90°

Le soleil parcourt 90 – 89,75 = 0,25° ce qui demande 1 min.

La durée du demi-coucher est de 1 min ; le coucher dure 2 minutes. C’est bien ce qu’on avait vu plus haut.

A.III.b -Aux solstices

La déclinaison du soleil est de ± 23,4°. On a sin(23,4°) = 0,397148 et cos(23,4°) = 0,917754

sin(h) = cos(23,4) x cos(H)

cos(H) = sin(h) / cos(23,4°)

Au début du coucher, h_D = 0,25° ; sin(h_D) = 0,004363

cos(H_D) = 0,004363 / 0,917754 = 0,004754

H_D = arccos(0,004754) = 89,727°

À mi-coucher h_mc = 0 donc sin(h_mc) = 0 donc cos(H)= 0 donc H_mc = 90°

Le soleil parcourt 90 – 89,727 = 0,273° ce qui demande

0,273 x 4 = 1,092 min .

Le coucher dure 2 x 1,092 min = 2,184 min = 131s.