D -En France à 45° de latitude

Cette latitude est relativement centrale en France et bien commode car sin(L) = cos(L) = 1 / √2 = 0,707 (ce qui est précis à 1,5/10000).

La figure 2 montre les trajectoires des étoiles et du soleil  sous 45° de latitude coté sud.

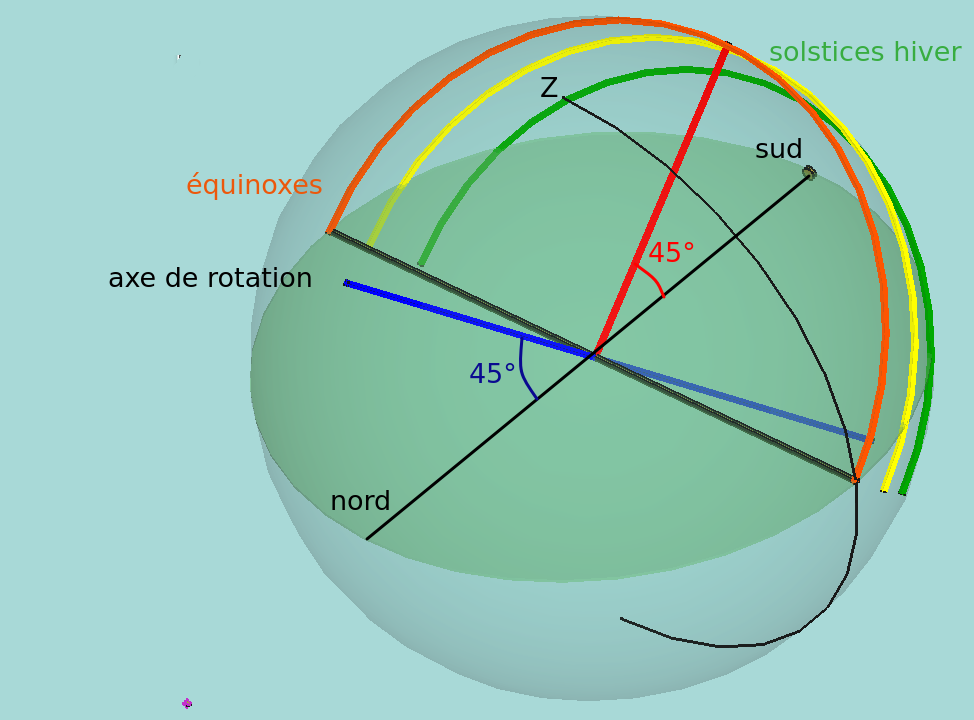
Figure 2

Ici, seul le demi-cercle rouge a son centre au niveau du sol. Les centres des arcs jaune et vert sont enfoncés dans le sol. Ils sont sur l'axe de rotation de la terre qui est incliné de 90° par rapport à la ligne droite rouge ( On triche un tout petit peu en le translatant au point d'observation).. Ainsi on en voit moins d'un demi-cercle.Le coucher à lieu avant H = 90°.

Pour les arcs symétriques, coté nord (non représentés), c'est le contraire. Leurs centres sont au-dessus du sol et donc on en voit plus de la moitié..Le coucher à lieu au-delà de  H = 90°.

Figure 3

On a :

sin(h) = 0,707 x sin(D) + 0,707 x cos(D) x cos(H)

sin(h) – 0,707 x sin(D) = 0,707 x cos(D) x cos(H)

cos(H) = (sin(h) – (0,707 x sin(D)) / (0,707 x cos(D))

D.I -Aux équinoxes

À mi-coucher H_mc=90° (horizon ouest).

D = 0 donc sin(D) = 0 et cos(D) = 1 ce qui nous donne :

cos(H) = sin(h) / 0,707 = sin(h) x √2

et comme h est très petit :

cos(H) = h x √2 (h en radians)

Au début du coucher, h= 0,004363 rd

cos(H_D ) = 0,004363 x √2 =0,06170

H_D = arccos(0,006170) = 89,646°

À mi-coucher H_mc=90° (horizon ouest, demi-cercle rouge de la figure 2))

Le demi-coucher s’étend sur 90 – 89,646 = 0,3536°

Il dure 0,3536 * 4 = 1,414 min*

Sous 45° de latitude, aux équinoxes, le coucher dure √2 fois plus longtemps qu’à l’équateur soit 2,83min = 170s.

Ceci peut se comprendre en reconsidérant la figure 2. Le cercle rouge est incliné de 45° ; pour s’élever de h° il faut parcourir h x √2° sur le cercle.

(l'hypoténuse d'un triangle rectangle isocèle mesure √2 fois les cotés de l'angle droit). On peut généraliser facilement : Aux équinoxes, le coucher dure 2 min / cos(L) .

D.II -Au solstice d’été

La déclinaison du soleil est de 23,4° ; sin(D)= 0,39715 et cos(D)= 0,91775.³

Au début du coucher, sin(h_D) = 0,004363

­rappel cos(H_D) = (sin(h_D) – 0,707 x sin(D)) / 0,707 x cos(D)

En séparant les 2 termes de la soustraction :

cos(H_D) = ( sin(h_D) x √2 / cos(D) ) – (sin(D) / cos(D))

cos(H_D) = 0,00672320 – 0,432743

cos(H_D) = -0,42602

H_D = arccos(-0,42602) = 115,21°

À mi-coucher, le premier terme de la soustraction disparaît

cos(H₀) = -0,432743

H₀= arccos(-0,432743) = 115,64°

Le demi-coucher s’étend sur 115,64 – 115,21 = 0,43° ce qui correspond à 1,72min

Sous 45° de latitude, au solstice d'été, le coucher dure 3,440 min = 206 s .

D.III -Au solstice d’hiver

La déclinaison du soleil est de -23,4° ; seul sin(D) change (de signe) = -0,39715.

Au début du coucher, La soustraction précédente devient une addition en prenant la valeur absolue de sin(D).

cos(H_D) = ( sin(h_D) x √2 / cos(D) ) + (sin(D) / cos(D))

cos(H_D) = 0,00672320 + 0,432743

Comme le premier terme est très petit en valeur absolue par rapport au second, la valeur de la somme est pratiquement identique (au signe près) à celle de la soustraction du solstice d’été.

cos(H_D) = 0,439466

H_D= arccos(0,439466) = 63,93°

À mi-coucher, cos(H₀) = 0,28079 / 0,64885 = 0,43275

H₀= arccos(0,43275) = 64,36°

Le demi-coucher s’étend sur 64,36 – 63,93 = 0,43° ce qui correspond à 1,72min

Sous 45° de latitude, au solsticee d'hiver, le coucher dure 3,44 min = 206s