Définir un cercle de rayon connu
Avril 2021. Par ces temps de semi-confinement, on est autorisé à circuler en France dans un rayon de 10km à vol d’oiseau (30 par dérogation), autour de chez soit. Cet article vous propose de déterminer jusqu’où vous pouvez aller en plaçant sur une carte des épingles suivant un cercle de rayon déterminé centré sur votre lieu d’habitation.
April 2021. During this time of semi-containment, you are allowed to travel in France within a 10km radius as the crow flies (30 by derogation), around your home. This article proposes you to determine how far you can go by drawing on a map a circle of determined radius centered on your place of residence.
Faire la carte
Pour obtenir la bonne carte, je vous propose d’utiliser Framacarte.
Vous pourrez trouver ici les bases de l’utilisation de Framacarte :
https://framablog.org/2016/03/04/comment-creer-sa-premiere-framacarte-tutos-umap-24/
Débutez donc une nouvelle carte > À droite choisissez le fond de carte qui convient en cliquant sur la pile de feuille : Openstreetmap.fr. Faites des clic-gl jusqu’à placer votre lieu de résidence au centre de la carte. Zoomez fort avec les gros + et – en haut à gauche de façon à situer votre lieu de résidence.
Voilà, vous avez la carte qu’il vous faut.
Notez vos coordonnées
clic sur l'outil marqueur (en haut à droite). Poser un marqueur à l'endroit choisi. Dans les propriétés choisissez coordonnées en bas et notez les valeurs indiquées sans les modifier! 4 chiffres derrière la virgule suffiront. Retirez le marqueur. Laissez la carte ouverte.
Ouvrez ce classeur:
Il est en lecture seulement. Clic sur éditer. On vous demande ce qui doit être effacé: cochez les nombres.
Inscrivez la longitude et la latitude notées en E1 et E2. Utilisez des points décimaux pas des virgules.
Indiquez le rayon du cercle en km en F6.
Faites M Données > sélectionner la plage > Valider > copiez la sélection.
Retournez sur votre carte. Clic sur gérer les calques (la pile de disques) > clic sur le + > appelez le cercleXXkm. > plus bas forme de l’icône : choisissez épingle > le reste se comprend facilement, je vous laisse faire. > fermer.
Clic sur la flèche montante au-dessus de la roue dentée > choisissez votre calque cercleXXkm (mais ça devrait être déjà fait) > format des données : csv > dans la petite fenêtre sous renseigner une URL faites [Ctrl] + [V] pour coller vos données. > clic sur importer et voyez le travail !
En vidéo ici: (sans son, ça colle au texte)
Pour faire une autre carte avec un autre cercle centré sur d’autres coordonnées, vous n’avez qu’à changer le contenu des cellules E1 et E2 et refaire une importation.
Voyez le résultat au complet et à l'échelle 5km.
NB: Faites clic-d (dans l'image) > afficher l'image pour obtenir la résolution native de l'image.
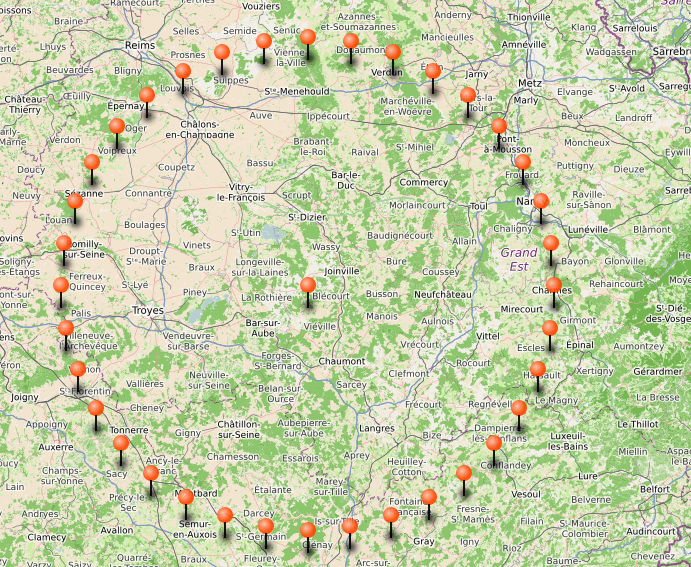
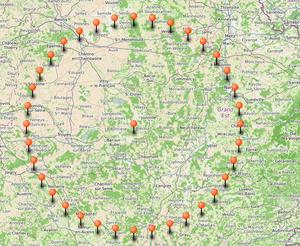
une autre zoomable à souhait:
Pour les matheux
Explications concernant le tableur
Nous allons placer une épingle tous les 10° soit 36 au total (plus une au centre).
Le rayon de la terre est d’environ 6367km (moyenne entre le rayon équatorial et le rayon polaire). La circonférence est donc de 40008km et 1° correspond à 111,13km (40008/360). On en déduit que 100km correspondent à 0,9° à très peu près et 1km à 0,009°.
-Première approche
Supposons que vous soyez au point de latitude 0° et longitude 0° donc sur l’équateur. On écrira 0;0. Appelons C ce point.
Si, depuis C :
-
Vous faites 100km à l’est vous serez au point E 0° ; 0,9°. La direction de E est 0°.
-
Vous faites 100km à l’ouest vous serez au point O 0° ; -0,9°. La direction de O est 180°
-
Vous faites 100km au nord vous serez au point 0,9° ; 0°. Soit N ce point. De direction 90°.
-
Vous faites 100km au sud vous serez au point -0,9° ; 0°. Soit S ce point. De direction 270°.
-
Vous faites 100km dans une direction d comptée dans le sens trigonométrique avec CE comme origine. Vous êtes au point P de coordonnées 0,9 sin(d) ; 0,9 cos(d).
Supposons maintenant qu’on parte du point C1 de coordonnées 2°; 3°. Le point P1 se calcule en ajoutant les coordonnées de C1 soit 2+0,9sin(d) ; 3+0,9cos(d).
En France
Quittons les chaleurs équatoriales pour la France. Plaçons nous au point 47° ;6°. Il y a maintenant un problème supplémentaire : Le parallèle de latitude 47° a un rayon nettement plus petit que R0 celui de l’équateur. Il vaut R0 cos(47°).
Les coordonnées de P sont donc 47 + 0,9 sin(d) ; 6 + 0,9 /cos(47) .cos(d).
Mais nous avons fait une petite approximation : Ce n’est pas cos(47) qu’il fallait prendre en toute rigueur mais cos( la latitude de P).
Finalement, cas général :
latitude P : La = Lac + 0,9 sin(d)
longitude P : Lo = Loc + 0,9 / cos(La) . cos (d)
où Lac et Loc sont respectivement la latitude et la longitude du centre, donc de votre lieu d’habitation.
E.II -Le tableur
Il est maintenant facile de faire un tableau des positions de 10° en 10°.
Pour un rayon de R km, il faudra remplacer le coeficient 0,9 des formules ci-dessus par 0.009 x R
***** © M Guignard *****

Comments powered by CComment