Tracé de l’exponentielle adaptée à votre cas personnel:
Dans l’exemple donné plus haut, 20cm d’ordonnées correspondent à 20° et à une puissance de 5kW.
Pour vous, cette puissance P20 n’est pas très facile à déterminer. Si vous vous chauffez à l’électricité, une solution consiste à arrêter tous les appareils électriques sauf bien entendu les radiateurs électriques, relever le compteur et la température extérieure, attendre une heure (au moins) , relever à nouveau le compteur et la température extérieure. Soit E la quantité d’énergie consommée en kWh en 1heure et T l’écart moyen entre la température intérieure et la température extérieure.
P20 = E / T × 20.
Chaque cm d’ordonnée correspond à 1° mais aussi à Pu = P20 / 20.
Si vous vous chauffez au fuel, une jauge avec un simple flotteur ne suffira pas, il faut disposer d’un compteur donnant une résolution au 1/10e ou du 1/100e de litre. Je crains que peu d’’installations en aie, ça coûte quand même facilement 600€. Dans ce cas, vous compterez non pas des kWh mais des litres facilement convertibles en €.
Il vous faut aussi déterminer ϴ :
Laisser refroidir un temps suffisant pour perdre 1° ou 2°.
ϴ = 20 × T1° ou 10 × T2° approximativement
Pour plus d’exactitude prenez la formule plus haut : ϴ = t / ln(T0 / T).
NB :ln est le logarithme népérien. Certaines calculettes le donnent d’autres vous donnerons seulement le logarithme décimal noté log.
Dans ce cas, la formule devient : ϴ = t × 2,3 / log(T0 / T).
Vous pouvez aussi utiliser Calc ou Excel.
Avec cette formule, plus vous laisserez refroidir, plus la valeur de ϴ sera précise.
Il faut maintenant établir un tableau qui s’adapte à tous les cas.
voici ce tableau (partiel) obtenu avec Calc (ou Excel) qui montre non pas les valeurs calculées mais les formules à inscrire.
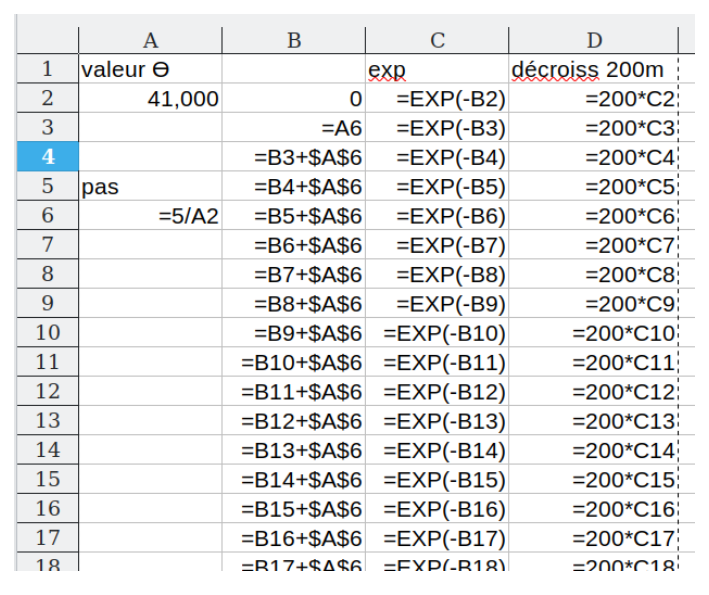
La valeur de ϴ doit être entrée en A2 (ici 41h).
L’exposant de l’exponentielle s’écrit E = -n × t / ϴ avec n qui augmente de 1 à chaque ligne. Mais le temps doit augmenter de 5h d’une ligne à la suivante quelque soit ϴ, pour faciliter l’usage du graphe. Donc l’exposant doit augmenter de pas = 5 / ϴ à chaque fois d’ou le contenu de A6.
Voici le même tableau avec les valeurs numériques pour ϴ = 41h.
|
valeur ϴ |
exposant |
exponentielle |
ordonnées |
|
41,000 |
0,000 |
1,000 |
200,0 |
|
|
0,122 |
0,885 |
177,0 |
|
|
0,244 |
0,784 |
156,7 |
|
pas |
0,366 |
0,694 |
138,7 |
|
0,122 |
0,488 |
0,614 |
122,8 |
|
|
0,610 |
0,543 |
108,7 |
|
|
0,732 |
0,481 |
96,2 |
|
|
0,854 |
0,426 |
85,2 |
|
|
0,976 |
0,377 |
75,4 |
|
|
1,098 |
0,334 |
66,7 |
|
|
1,220 |
0,295 |
59,1 |
|
|
1,341 |
0,261 |
52,3 |
|
|
1,463 |
0,231 |
46,3 |
|
|
1,585 |
0,205 |
41,0 |
|
|
1,707 |
0,181 |
36,3 |
|
|
1,829 |
0,161 |
32,1 |
|
|
1,951 |
0,142 |
28,4 |
|
|
2,073 |
0,126 |
25,2 |
|
|
2,195 |
0,111 |
22,3 |
|
|
2,317 |
0,099 |
19,7 |
|
|
2,439 |
0,087 |
17,4 |
Dans Librecad, on choisi le mm comme unité et on prépare un graphe ayant pour origine celle du dessin, repérée par une croix rouge dans Librecad, avec un axe des y de 200mm de haut (chaque cm correspond à 1°) et un axe des x (en fait des temps) de 400 mm à réajuster plus tard éventuellement.
On prend l’outil qui trace des lignes verticales de longueur prédéfinie.
On règle la grille à 20mm et on accroche à la grille.
On se réfère à la 4e colonne du tableau.
On fixe la longueur à 177, l’origine à « début » et on place le curseur sur l’axe des temps à t = 5h donc x = 2cm. On clique.
On fixe la longueur à 156,7 l’origine à « début » et on place le curseur sur l’axe des temps à t = 10h donc x = 4cm. On clique.
On continue jusqu’en bas du tableau.
On obtient une bonne approximation de la courbe en joignant les extrémités des verticales par des segments de droites. Le résultat serait meilleur avec des splines mais celles-ci ne se prêtent pas aux opérations suivantes.
4cm d’abscisse correspondent à 10h ; 1cm = 2,5h ; 1h = 4mm.
Rappel : Chaque cm d’ordonnée correspond à Pu = P20 / 20.
On va se fixer ici P20 = 6kW pour l’exemple, donc : Pu = 0,3kW/°
donc 1cm2 de surface correspond à
Eu = Pu × 2,5 kWh. = 0,75 kWh

Comments powered by CComment