faut il couper le chauffage quand on quitte son logement

Faut il couper le chauffage quand on quitte son logement ?

Par ces temps d’énergie de plus en plus chère, la question mérite d’être posée, même si la réponse n’est pas simple.

NB : Cet article est long et un peu ardu. Les plus impatients pouront sauter directement au dernier paragraphe.

In these times of increasingly expensive energy, the question is worth asking, even if the answer isn't easy.

NB: This article is long and somewhat arduous. Impatient readers can skip to the last paragraph.

Dans une première approche on va partir sur les données suivantes :

Un logement demande 5kW pour être maintenu à 20° avec une température extérieure de 0°.

1. Les pertes sont donc de 5 / 20 = 0,25kW par degrés d’écart. Retenons bien cette valeur.
2. On constate que si on coupe le chauffage pendant 10h d’absence, la température descend de 2°.

Quelle est l’économie réalisée ?

Au bout des 10h, la différence de température intérieure-extérieure est de 18°. Comme les pertes sont proportionnelles à cette différence, la puissance des pertes est tombée à 0,25 × 18 = 4,5kW.

La température ne chute pas linéairement mais suivant une exponentielle (on verra ça plus loin), mais comme la chute est relativement faible, on la considérera comme linéaire dans un premier temps.

Dans ces conditions, la puissance moyenne des pertes s’élève à (5 + 4,5) / 2 = 4,75kW.

L’énergie perdue sur les 10h est de 4,75 × 10 = 47,5kWh.

Si on avait continué à chauffer on aurait consommé 50kWh ; on a donc économisé 50 – 47,5 = 2,5 kWh.

À 25cts le kWh on gagnerait 62,5cts par jour soit 18,75€ sur un mois de 30jours.

Ceci appelle quelques remarques :

• Il ne fait pas 0° 24h/24 pendant toute la période de chauffage. Par exemple, de janvier à avril la température moyenne est d’environ 5,5° à Besançon.
• Est ce qu’on accepte de rentrer dans un appartement à 18° ?

Alors reprenons nos calculs :

La différence de température dt est maintenant de 20 – 5,5 = 14,5°.

Les pertes s’élèvent à 0,25 × 14,5 = 3,62kW.

En 10h on va perdre environ 2° / 20 × dt = 1,45°. La différence de température intérieure-extérieure finale est de 14,5 – 1,45 = 13°.

Avec 13° d’écart, les pertes tombent à 0,25 × 13 = 3,25kW.

La moyenne est de (3,62 + 3,25) /2 = 3,43 kw.

Sur les 10h les pertes sont de 34,3 kWh. En maintenant le chauffage, on aurait dépensé 36,2kWh.

On a donc économisé 36,2 – 34,3 = 1,9kWh soit 47,5c€ / jour donc 14,25€ sur un mois. La température chute à 20 – 1,45 = 18,6°.

Méthode graphique

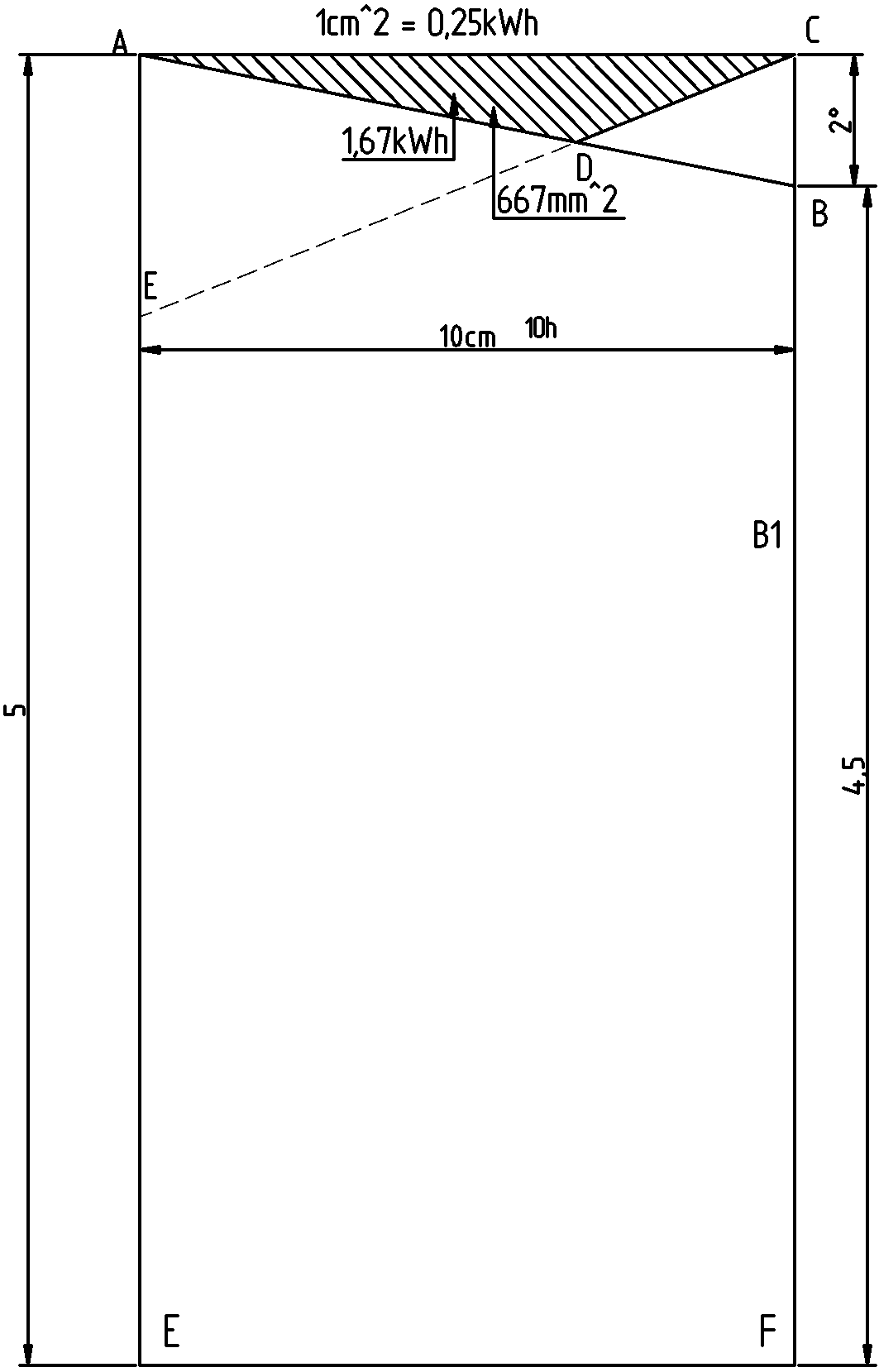
Figure 1 :

On utilise un logiciel de dessin technique. Librecad. pour moi.

Examinons le dessin ci-dessus. La ligne verticale AE fait 20cm de haut. Cette longueur représente 20° mais aussi une puissance de 5kw. On s’est arrangé pour que la cotation affiche directement cette puissance en ajustant un paramètre de cotation.

La ligne AB représente la chute de température. La cotation de BF nous donne directement la puissance des pertes au bout des 10h.

Chaque cm correspond à 0,25kW en hauteur et 1h en largeur, donc 1cm² représente 0,25kWh. La surface du triangle ABC, facile à calculer, nous donne les kWh économisés en multipliant son expression en cm² par 0,25, si on accepte de rentrer dans un logement à 18°.

La droite EC a une pente double de celle de AB car on admet que la puissance maximale de chauffage est le double de celle nécessaire pour maintenir nos 20°. On la construit en partant de C. La surface du triangle ACD nous donne l’énergie économisée avec un logement réchauffé. Avec Librecad on peut la mesurer facilement.

Essayons de généraliser

Jusqu’ici nous nous sommes penchés sur deux cas particuliers supposés et en simplifiant les calculs. Essayons de passer à un graphe plus général qui s’adapterait à des pertes quelconques et sur des durées diverses.

La physique nous enseigne qu’en réalité la chute de température suit une loi exponentielle négative.

T=T₀ ×e^(-t/ϴ)

T₀ est la température de départ (20°) en fait, c’est l’écart de température intérieur-extérieur au départ, on y reviendra ; t est le temps écoulé depuis la coupure du chauffage, e est un de ces nombre magique utilisés par les mathématiciens. Il vaut environ 2,718 . ϴ est la constante de temps. Ce temps est celui qu’il faudrait pour atteindre 0° si la chute de température se maintenait constamment au rythme de départ, plus précisément, c’est l’abscisse du point d’ordonnée 0 de la tangente à l’origine des temps . On en a une idée approximative en disant que s’il faut 10h pour perdre 2° alors il faudrait 100h pour perdre 20° ; ϴ ≈ 100h. En fait, on a remplacé la tangente par une petite corde.

La vraie valeur se calcule ainsi à partir de la formule ci-dessus:

on la met sous la forme :

T / T₀ = e^(-t/ϴ)

d’où l’on tire :

ln(T/ T₀) = -t/ϴ donc ln(T/ T₀) / -t = 1/ϴ

qu’on peut mettre sous la forme

ϴ = -t / ln(T/ T₀)

soit

ϴ = t / ln(T₀ / T) = t / (ln(T0) - ln(T))

Ce qui nous donne

ϴ = 10 / ln(20/18) = 10 / ln (1,111) = 95h

Nos 100h étaient justes à 5 % près.

Considérons le tableau ci-dessous.

La deuxième colonne calcule l’exponentielle. La formule est : =Exp(-A2) pour la ligne 2.

La troisième colonne calcule l’ordonnée de la courbe de décroissance en multipliant l’exponentielle par un simple coefficient . La fonction est =200 × B2 pour la ligne 2.

Le facteur 200 se justifie par les 200 mm représentant 20°.

Tracé de l’exponentielle adaptée à votre cas personnel:

Dans l’exemple donné plus haut, 20cm d’ordonnées correspondent à 20° et à une puissance de 5kW.

Pour vous, cette puissance P₂₀ n’est pas très facile à déterminer. Si vous vous chauffez à l’électricité, une solution consiste à arrêter tous les appareils électriques sauf bien entendu les radiateurs électriques, relever le compteur et la température extérieure, attendre une heure (au moins) , relever à nouveau le compteur et la température extérieure. Soit E la quantité d’énergie consommée en kWh en 1heure et T l’écart moyen entre la température intérieure et la température extérieure.

P₂₀ = E / T × 20.

Chaque cm d’ordonnée correspond à 1° mais aussi à     P_u = P₂₀ / 20.

Si vous vous chauffez au fuel, une jauge avec un simple flotteur ne suffira pas, il faut disposer d’un compteur donnant une résolution au 1/10e ou du 1/100e de litre. Je crains que peu d’’installations en aie, ça coûte quand même facilement 600€. Dans ce cas, vous compterez non pas des kWh mais des litres facilement convertibles en €.

Il vous faut aussi déterminer ϴ :

Laisser refroidir un temps suffisant pour perdre 1° ou 2°.

ϴ = 20 × T_1° ou 10 × T_2° approximativement

Pour plus d’exactitude prenez la formule plus haut : ϴ = t / ln(T₀ / T).

NB :ln est le logarithme népérien. Certaines calculettes le donnent d’autres vous donnerons seulement le logarithme décimal noté log.

Dans ce cas, la formule devient : ϴ = t × 2,3 / log(T₀ / T).

Vous pouvez aussi utiliser Calc ou Excel.

Avec cette formule, plus vous laisserez refroidir, plus la valeur de ϴ sera précise.

Il faut maintenant établir un tableau qui s’adapte à tous les cas.

voici ce tableau (partiel) obtenu avec Calc (ou Excel) qui montre non pas les valeurs calculées mais les formules à inscrire.

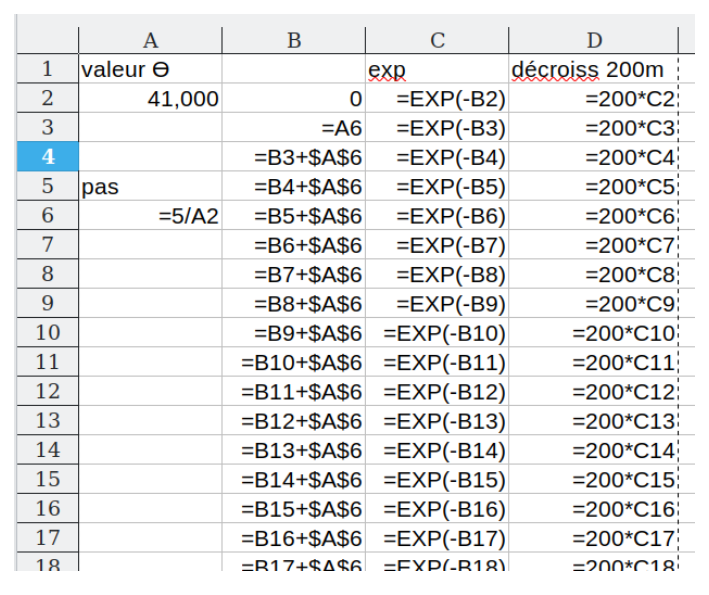
La valeur de ϴ doit être entrée en A2 (ici 41h).

L’exposant de l’exponentielle s’écrit E = -n × t / ϴ avec n qui augmente de 1 à chaque ligne. Mais le temps doit augmenter de 5h d’une ligne à la suivante quelque soit ϴ, pour faciliter l’usage du graphe. Donc l’exposant doit augmenter de pas = 5 / ϴ à chaque fois d’ou le contenu de A6.

Voici le même tableau avec les valeurs numériques pour ϴ = 41h.

Dans Librecad, on choisi le mm comme unité et on prépare un graphe ayant pour origine celle du dessin, repérée par une croix rouge dans Librecad, avec un axe des y de 200mm de haut (chaque cm correspond à 1°) et un axe des x (en fait des temps) de 400 mm à réajuster plus tard éventuellement.

On prend l’outil qui trace des lignes verticales de longueur prédéfinie.

On règle la grille à 20mm et on accroche à la grille.

On se réfère à la 4^e colonne du tableau.

On fixe la longueur à 177, l’origine à « début » et on place le curseur sur l’axe des temps à t = 5h donc x = 2cm. On clique.

On fixe la longueur à 156,7 l’origine à « début » et on place le curseur sur l’axe des temps à t = 10h donc x = 4cm. On clique.

On continue jusqu’en bas du tableau.

On obtient une bonne approximation de la courbe en joignant les extrémités des verticales par des segments de droites. Le résultat serait meilleur avec des splines mais celles-ci ne se prêtent pas aux opérations suivantes.

4cm d’abscisse correspondent à 10h ; 1cm = 2,5h ; 1h = 4mm.

Rappel : Chaque cm d’ordonnée correspond à P_u = P₂₀ / 20.

On va se fixer ici P₂₀ = 6kW pour l’exemple, donc : P_u = 0,3kW/°

donc 1cm2 de surface correspond à

E_u = P_u × 2,5 kWh. = 0,75 kWh

Comment utiliser la courbe

Le dessin ci-dessous montre ce qu’il faut faire. Notez que vous pouvez ouvrir l'image dans un nouvel onglet pour une meilleure visibilité.

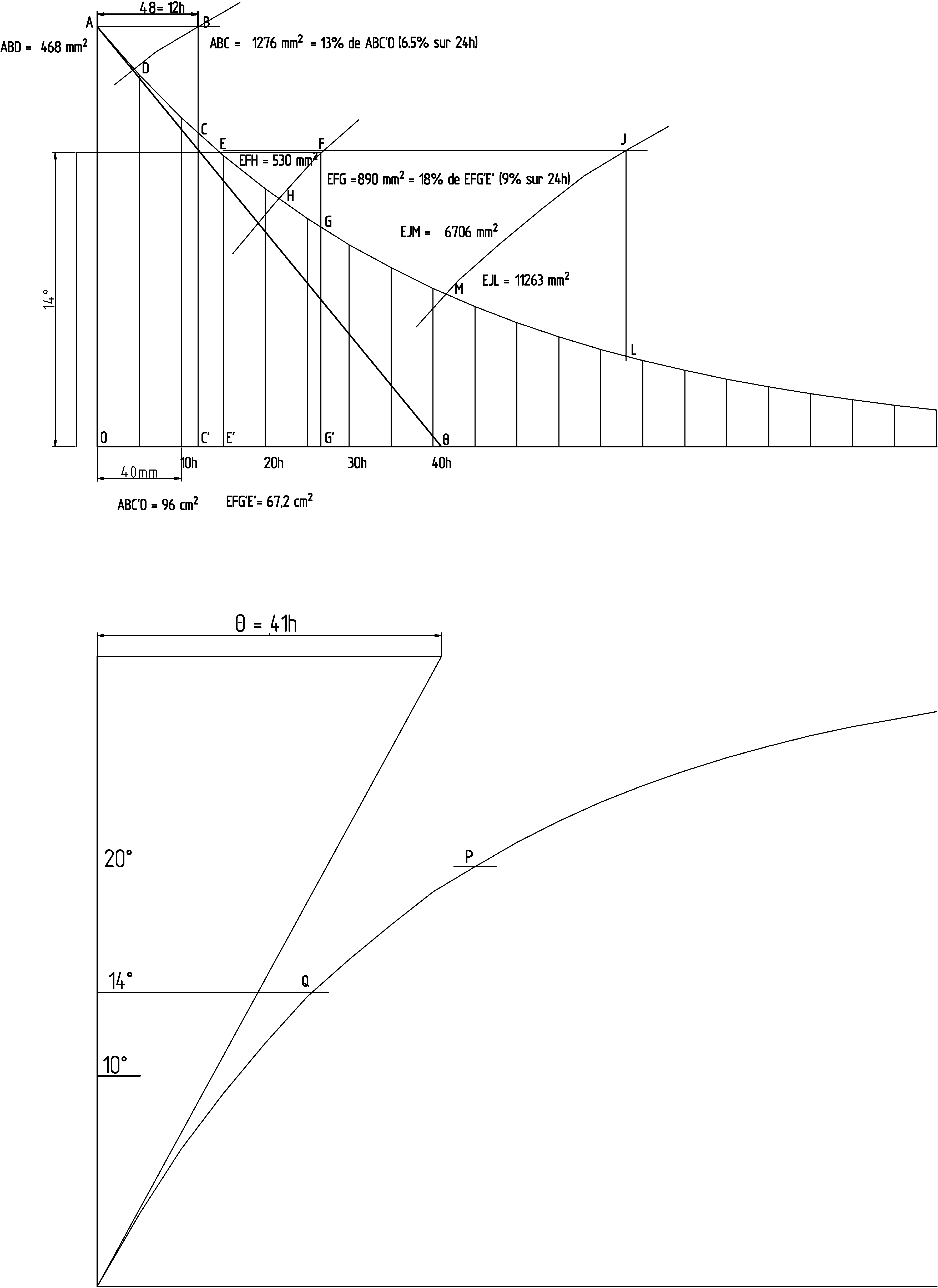
Figure2

Supposons qu’il fait 0° dehors 20° dedans et qu’on s’absente 12h.

On trace une horizontale de 48mm (12h) depuis le point A (0,200.). B est son extrémité On trace une verticale depuis B qui descend jusqu’à couper la courbe au point C et l’axe des temps en C’. La surface du pseudo triangle ABC se mesure avec l’outil appelé aire du polygone. On clique au point A puis au point B puis au point C et on revient sur A le long de la courbe. La valeur de la surface S s’affiche au-dessus de la ligne de commande en mm². L’énergie économisée est

E_e = S / 100 × E_u = 12,76 × 0,75 = 9,57 kWh.

Plus généralement, pour un écart de température de T_e° et une durée t on tracera une horizontale correspondant à cette température, 14° dans le dessin (donc d’ordonnée T_e cm), qui coupera la courbe au point E et qui se prolongera au-delà de E d’une longueur de t × 4 mm, 48mm dans le dessin nous donnant le point F.

La verticale issue de F coupe la courbe en G et l’axe des temps en G’.

La surface du pseudo triangle EFG nous permet de calculer les kWh économisés comme ci-dessus.

E_e14= 8,9 × 0,75 = 6,67 kWh

Si on réchauffe le logement avant de rentrer :

Il nous faut tracer la courbe de remontée en température.

Soit P_M la puissance disponible. Avec une puissance P₂₀ on maintient un écart de 20°, donc avec PM on pourrait arriver à un écart de

D_M = 20 / P₂₀ × P_M.

Nous devons donc créer une exponentielle dont l’asymptote sera à D_M cm de hauteur ; sa constante de temps sera la valeur ϴ déterminée précédemment.

On part du tableur précédent. On ajoute Dmax en A8 et la valeur D_M en A9.

En D2 on écrit =$A$9*10*(1-C2). On valide la cellule on revient dedans et on tire le petit carré vers le bas.

On reprend le dessin de la courbe précédente et dans un autre endroit on trace deux axes xy comme précédemment mais avec l’axe y qui monte jusqu’a D_M × 10 mm.

Comme pour la courbe décroissante, on reporte des segments aux longueurs données par D3, D4, D5… tout les 20mm. Puis on trace la courbe qui joint les extrémités des segments, puis on efface ces segments.

Comment utiliser la courbe de réchauffage :

Donnons un exemple concret ce sera plus facile.

L’écart intérieur extérieur à atteindre est de 14° (par exemple on veut 19° et il fait 5° dehors).

On trace sur la courbe croissante l’horizontale à 14° qui vient couper la courbe en Q

Sur la courbe croissante on sélectionne les segments de part et d’autre de Q.

On prend l’outil de copie. On nous demande le point de référence. On désigne Q. On nous demande le point de destination. On désigne le point F placé précédemment.

Le bout de courbe croissante coupe la courbe décroissante en J. Les économies correspondent maintenant à la surface EFH. Les économie sont maintenant

E_e14r = 0,75 × 5,3 = 3,97 kWh.

Partons en week-end

Le dessin étudie ce qu’il se passe sur une absence de 48h avec encore 14° d’écart. Je ne détaille pas voyez les points J,L et M.

Les économies relatives :

Elles ont été calculées et montrées dans le dessin en comparant les surfaces concernées. On a calculé le pourcentage sur les 12h d’absence. Évidemment pour un calcul sur la journée il faut diviser la valeur précédente par 2 puisque les journées font 2 fois 12h.

Ces données sont elles fiables ?

En théorie pure je pense que oui. Mais les données ne sont à l’évidence pas très réalistes. La température varie au cours des journées, parfois même beaucoup. La température d’un logement est rarement uniforme. Comment définir l’instant de ré-allumage du chauffage. Il faudra donc considérer vos résultats comme un ordre de grandeur. Mais ce ne sera certainement pas pire que les informations d’ENEDIS et compagnie...

Pour faire simple

Je vous ai donné dans cet article les moyens de calculer vos économies éventuelles. C'était un peu long et indigeste pour certains.

Voici la réponse simple à la question posée dans le titre:

Si pendant votre absence vous perdez 2° ou plus, vous ferez des économies notables en coupant le chauffage.

***** © M Guignard 2024 *****