Utilisation du viseur déporté avec une monture équatoriale

Le viseur décrit dans cet article est il utilisable avec une monture équatoriale ? À priori non... et pourtant...

Nous allons voir que cet instrument peut être exploitable moyennant l'acceptation d'une certaine méthodologie.

Is the viewfinder described in this article usable with an equatorial mount? Apparently not... but...

We will see that this device can be exploitable with the acceptance of a certain methodology.

Utilité du viseur

Normalement, avec une monture équatoriale on n'a pas trop besoin de viser, puisqu'on pointe aux coordonnées. Oui mais :

• Il faut viser l'étoile polaire pour débuter la mise en station. Noter que les axes de rotation qu’on utilise alors sont équivalents à ceux d'une monture azimutale.

• Il faut d'abord pointer une étoile connue pour régler le cercle gradué des ascensions droites.

• Avec l'accumulation des erreurs, on tombe parfois à coté !

• Il arrive que l'on ne connaisse pas les coordonnées équatoriales.

Des conditions d'utilisation variées

Les conditions d'utilisation changent suivant les régions du ciel. Il y a des positions dans le ciel où l'utilisation du viseur ne pose pas ou peu de problèmes. Notez que chaque fois que la hauteur est facile à modifier, l’azimut l’est aussi avec l’autre axe et inversement.

Au méridien, la hauteur se modifie en agissant uniquement sur l'axe de déclinaison (axe D).

Aux environs de l'étoile polaire, sur l'horizontale passant par celle-ci, la hauteur se change en agissant uniquement sur l'axe AD.

Dès lors, la question est de savoir ce qu'il se passe quand on s'éloigne plus ou moins modérément de ces positions idéales. On peut légitimement supposer que l'on va rencontrer des zones ''à dominante D'' (j'appelle ainsi les zones où un changement de hauteur s'obtient en modifiant essentiellement la déclinaison) et des zones ''à dominante H'' (où la hauteur se modifie en changeant essentiellement l'angle horaire H par rotation de l'axe AD).

Le rapport de domination de la déclinaison,

kD = dD / dH¹

est infini au méridien et décroît progressivement quand on s'en éloigne. Quand kD devient égal à 1, il n'y a évidemment plus de dominante.

Le rapport de domination de H, kH = dH / dD = 1/ kD est infini à l'horizontale du pôle céleste.

Il faut donc connaître le rapport de domination en chaque point du ciel et établir des stratégies d'approche en fonction de ce rapport.

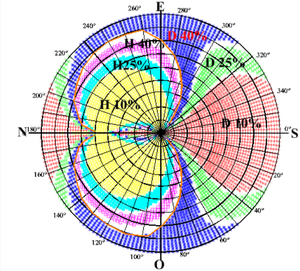
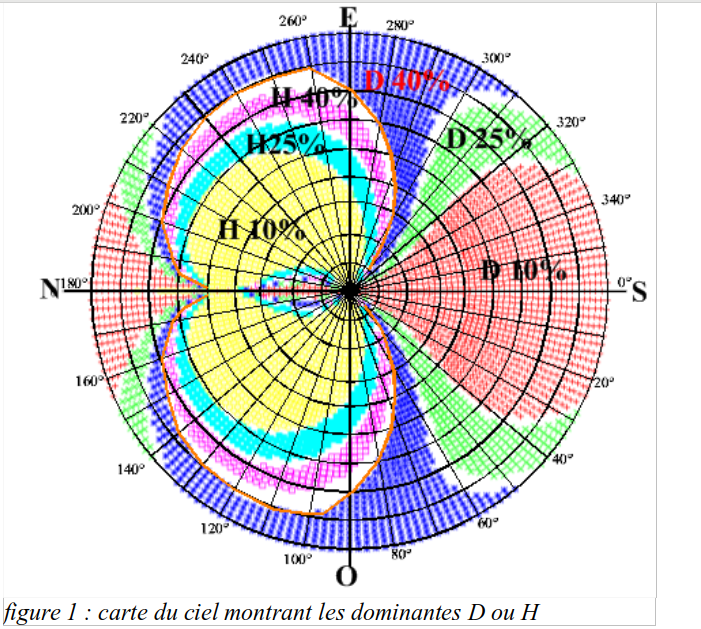La figure 1 présente une carte du ciel complet, la figure 2 détaille la zone autour du zénith et du pôle céleste où le rapport k change rapidement.

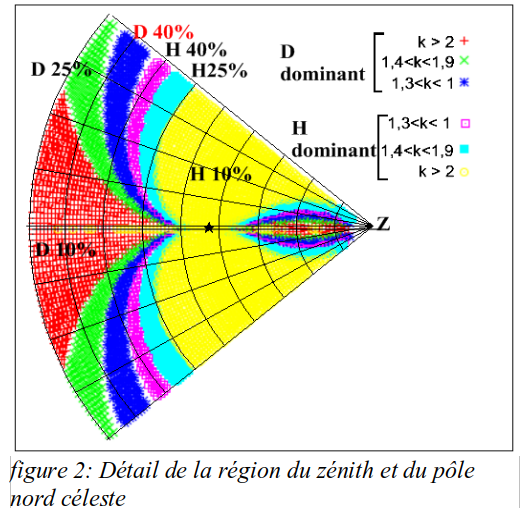Six zones ont été mise en évidence.

• La zone rouge correspond à kD supérieure à 2 (la déclinaison domine largement).

• La zone verte correspond à kD compris entre 1,9 et 1,4 (la déclinaison domine moyennement).

• La zone bleue correspond à kD compris entre 1,3 et 1 (la déclinaison domine faiblement ou pas du tout.

• La zone mauve correspond à kH compris entre 1,3 et 1,1 (H domine faiblement)

• La zone bleu clair correspond à kH compris entre 1,9 et 1,4 (H domine moyennement) .

• La zone jaune correspond à kH supérieur à 2 (H domine largement).

On remarque qu'il existe deux grandes zones (rouge et jaune) à dominante bien marquée. La zone bleue est relativement importante mais si on exclut les vingt premiers degrés de hauteur où les observations sont de mauvaise qualité, il n'en reste plus grand chose.

Une stratégie d'approche par corrections alternatives sur les deux axes est donc indispensable et la question se pose de savoir quel est le meilleur parcours pour atteindre le but le plus rapidement possible ?

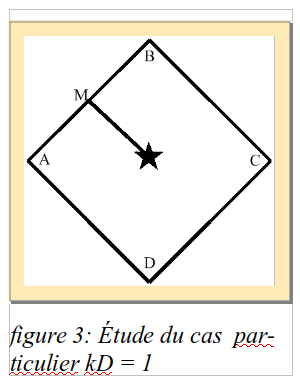
Considérons d'abord le cas le plus critique où kD = kH = 1. Dans la figure 3, on part (point A) d'une situation facile à créer ou l'une des coordonnées (ici la hauteur) est ajustée correctement. On voit que si on corrige complètement l'azimut, par exemple avec l'axe D, alors l'erreur est transférée sur la hauteur avec la même valeur (point B). Si on alterne ensuite les axes, on va tourner indéfiniment autour de l'étoile à atteindre en décrivant un carré ABCD. Notons toutefois qu'il s'agit d'une situation non réaliste, car en fait la valeur kH = 1 ne se rencontre pas sur une grande étendue.

Dans le cas envisagé, la bonne stratégie consiste à reculer de la moitié de la correction(de B en M) avant de corriger entièrement la hauteur (et simultanément l'azimut), avec l'autre axe.

En fait, cette technique peut être généralisée à tous les cas, à condition d'adapter le coefficient de recul suivant la valeur de kD ou kAD.

En pratique, un recul moyen est pré-calculé pour chaque couleur de zone et inscrit sur les cartes.

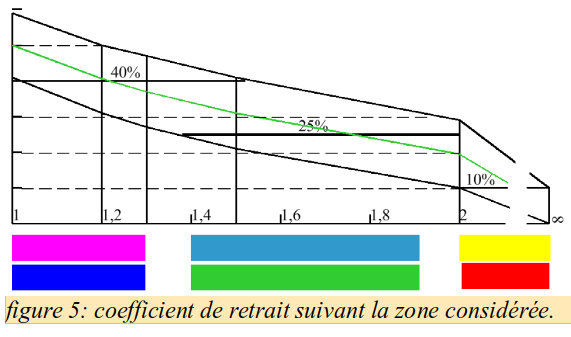
En réalité, le champ du chercheur ayant une étendue non négligeable, La zone de tolérance de k est relativement large. La figure 5 a été établi pour un écart de départ de 20° et en supposant que le champ du chercheur est de 5°. En tout état de cause, si l'on fait une erreur de 10% sur le coefficient de correction, l'écart de pointage sera tout de même atténué d'un facteur 10 après un cycle et d'un facteur 100 après 2 cycles. Même avec une erreur de 20% les atténuations sont encore de 5 et 25 ce qui signifie qu'en débutant le premier cycle avec un écart de 20°, on terminera à moins d' un degré de la cible.

 Diverses situations

Pour le pointage de l'étoile polaire (m.e.s.): on utilise la monture comme une azimutale sans aucun problème. Si on observe toujours dans une zone géographique limitée, on pourra faire sur l’inclinomètre une marque sur la graduation correspondant à la latitude du lieu d'observation. Le réglage en hauteur (latitude) se fera alors sans visée en posant directement le viseur sur le télescope. Pour l'azimut, on pourra viser, non pas l'étoile polaire, mais la position estimée du pôle céleste, à 0,75° de Polaris, sur la ligne Polaris - δ du dragon.

Pour le réglage du cercle des AD : il faut viser une étoile connue, de son choix. On en profitera pour choisir une étoile bien placée, dans une zone rouge ou jaune où le facteur kD ou kH est élevé. On commencera par régler D suivant les graduations de la monture. Ensuite :

• Si on est en zone rouge, on réglera l'axe AD sur l'azimut de l'étoile. À ce moment là, on devrait, avoir ou être sur le point d'avoir l'étoile cible dans le champ du chercheur. En retouchant la déclinaison de façon à ajuster la hauteur, on devrait atteindre l'astre choisi. 

• si on est en zone jaune, on réglera l'axe AD sur la hauteur. À ce moment là, on devrait, avoir ou être sur le point d'avoir l'étoile cible dans le champ. En retouchant l'AD de façon à ajuster l’azimut, on devrait atteindre l'astre choisi. 

Dans le cas d'un pointage aux coordonnées équatoriales raté, on devrait être assez près de la bonne position. On commencera par annuler l'erreur d'azimut :

• Si on est en zone rouge, verte, ou bleue (dominante D), on règle l'axe AD sur l'azimut de l'étoile. Ensuite on corrige complètement la hauteur avec l'axe D, puis on revient en arrière de x% de la correction (x est à lire sur les cartes dans la zone concernée). On refait l'égalité de l'azimut avec l'axe AD. En principe l’étoile devrait être dans le champ du chercheur donc s’il est nécessaire de refaire un cycle, on agira sur l’axe AD jusqu’à ce que l’étoile passe au plus près du centre du champ puis sur l’axe D pour un ajustement parfait. Normalement, on ne devrait pas avoir besoin d'un autre cycle.

• Si on est en zone jaune, bleu clair ou mauve (dominante H),on règle l'axe D sur l'azimut de l'étoile. Ensuite on corrige complètement la hauteur avec l'axe AD puis on revient en arrière de x% de la correction (x est à lire sur les cartes dans la zone concernée)). On refait l'égalité de l'azimut avec l'axe D. En principe l’étoile devrait être dans le champ du chercheur donc s’il est nécessaire de refaire un cycle, on agira sur l’axe D jusqu’à ce que l’étoile passe au plus près du centre du champ puis sur l’axe AD pour un ajustement parfait. Normalement, on ne devrait pas avoir besoin d'un autre cycle.

Si on ne connaît pas les coordonnées équatoriales, on peut commencer par évaluer la déclinaison : On mesure avec ses mains² la distance angulaire entre l'objet à pointer et l'étoile polaire. On obtient le complément de la déclinaison. On règle le télescope sur la déclinaison supposée, puis on tourne l'axe AD pour s'approcher le plus possible de la cible. On ne devrait alors pas être trop éloigné du but. On procède ensuite comme au paragraphe précédent.

On peut aussi envisager d'utiliser le viseur en sens inverse et ce n'est certainement pas l'aspect le moins intéressant de cette étude. On utilise le viseur, non pas pour se positionner sur une direction précise mais pour repérer la direction pointée par le télescope.

La démarche est simple. On pose l’inclinomètre sur le télescope pour lire la hauteur h. On prend le viseur en mains et on place le pouce pour qu'il vienne en butée sur l'index de l’inclinomètre quand celui-ci indique la valeur h. On aligne l’azimut du viseur sur l’axe optique du télescope et la hauteur pour perdre, mais tout juste, le contact entre votre pouce et l'index du viseur. On note alors les positions relatives du point P visé et de l'étoile E. Si le point P est plus éloignée de Polaris que l’étoile, il faut augmenter la déclinaison. Le sens de rotation de l'axe AD s'impose de lui même. On pourra évaluer à l’œil, ou avec ses mains, les angles de rotation des deux axes. Alternez mesure de la hauteur et correction de la déclinaison autant de fois qu’il sera nécessaire.

En conclusion, conçu au départ pour une utilisation avec un instrument à monture azimutale, le viseur déporté peut parfaitement rendre des services aux utilisateurs de montures équatoriales, à condition qu'ils veuillent bien s'astreindre à une démarche au fond tout à fait acceptable.

En dehors de l'utilisation de ce viseur, cette étude permettra aux débutants – et même à d'autres – de comprendre pourquoi ils se sentent entravés quand ils évoluent dans certaines régions du ciel, tandis qu'en d'autres endroits les choses paraissent plus faciles. Ils pourrons déduire de la consultation de la carte de la figure ,1 une démarche d'approche plus rationnelle.

====================================================================