Comment se courbe un fil tendu horizontalement
Quand on tend un long fil pour matérialiser une horizontale, on sait que celui-ci se courbe sous son poids. La matérialisation de l'horizontale n'est donc qu'approximative. Comment savoir de combien “ça creuse” et comment gérer au mieux ce type de problème. C'est ce que nous allons voir.

A -L'aspect matheux des choses
Ouhla ! Pas de panique, on va faire le moins de maths possible et ceux qui n'aiment pas (je sais, ils sont nombreux), pourrons toujours passer par-dessus. Mais ce serait dommage de ne pas expliquer un minimum aux autres...
Les physiciens nous disent que la courbe décrite par un fil tendu est un cosinus hyperbolique. Rien de moins ! Heureusement, les mathématiciens nous disent aussi qu'une telle courbe peut être approximée avec une très bonne précision par une simple parabole dès lors que le fil est bien tendu. Ouf !
Donc pour nous, la courbe décrite par le fil est du type y = a × x². L'origine des axes est placée au point milieu du fil donc au point le plus bas.
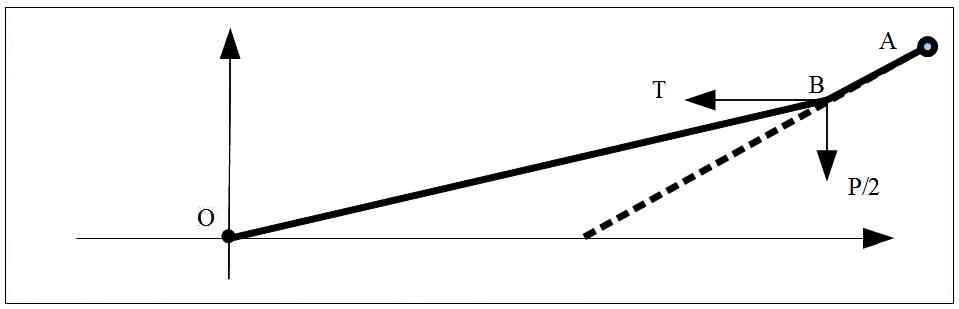
Pour comprendre ce qu'il se passe, il faut imaginer le dispositif suivant, où une moitié du fil est remplacé par une barre rigide pivotant à l'origine et l'extrémité par un chaînon rectiligne. Le chaînon AB est soumis à 2 forces perpendiculaires : la tension du fil T et une force égale au poids P du demi fil divisé par deux. En effet, le poids s'exerce au centre de gravité de la barre donc à mi-longueur, ce qui donne une force deux fois moindre au bout d'un bras de levier 2 fois plus grand. La pente que prends donc le chaînon est donné par le rapport p = (P/2) / T.
En réalité, cette direction représente la tangente de notre parabole à l'extrémité du fil. Or les maths nous enseignent que cette tangente coupe l'axe des x à mi-parcours. En d'autres termes, la courbe creuse 2 fois moins que si c'était une droite dans le prolongement de sa tangente à l'extrémité.
Concrétisons. Supposons un fil de 30m de long, pesant 30gr et tendu avec une force de 15kg. Le demi fil pèse 15gr donc P / 2 = 7,5 gr et la pente à l'extrémité vaut p = 7,5 / 15 000 = 0,000 5. Le creux en mm est donné par la distance au point d'origine (donc, la demi-longueur en mm) multipliée par la demi-pente.
Soit : h = 15 000 × 0,000 25 soit 7,5mm.
Formule pratique : h = P × L / T / 16
avec h en mm, P le poids du fil entier, L la distance entre les deux points d'attache en mm et T la tension du fil. P et T doivent être exprimés dans la même unité, en pratique en gr et tant pis pour les puristes qui diront que l'unité de force officielle est le Newton, les grammes sont autrement plus faciles à appréhender.
On peut aussi écrire, en faisant intervenir pu = le poids du fil par unité de longueur h = pu × L² / T /16.
B -Dans la réalité ça donne quoi ?
J'ai un fil de nylon de 8 centième de mm de diamètre qui résiste à une traction de 500gr. La densité du nylon est de l'ordre de 1,14. Où cela nous conduit il ?
Considérons une longueur de 50m. On tire dessus avec une force de 400gr pour garder un peu de marge.
La section du fil est de π × 0,008² /4 = 5 10-5cm² ou 0,00005cm²
Le volume du fil par cm de longueur est de 0,000 05cm3 et 100 fois plus pour 1m soit de 5.10‑3cm3 ou 0,005cm3 et le poids correspondant 0,005 × 1,14 = 0,005 73 gr par m soit 5,73mg par m.
Le poids du fil de 50m est donc de 5,73 10-3 × 50 = 0,29gr.
Donc h = 0,29 × 50 000 / 400 /16 = 2,2 mm.
Négligeable dans la majorité des cas. Mais le fil n'est pas facile à voir.
Pour ceux que les puissances de 10 embrouillent disons que le nylon supporte une traction de 100kg par mm². Un fil de 1mm de diamètre supporte 78kg ; un fil de 0,1mm casse au-delà de 780gr ; un fil de n dixièmes de mm résiste tout juste à n² fois 780gr.
Faut-il prendre un fil très fin ou plutôt gros ?
Si on double le diamètre du fil on multiplie la section par 4, la résistance à la traction par 4 et le poids par 4 donc on ne change rien... sauf que passer de 500gr à 2kg de traction ne me dérange pas, mais monter à 20kg commence à poser des problèmes. Donc, choisissons un fil plutôt fin mais autant que possible encore visible présentant un bon rapport résistance à la traction / poids. Le nylon et l'acier sont équivalents en résistance, mais l'acier est environ 7 fois plus lourd. Le fil d'araignée est encore bien meilleur, mais bon...
Ex : pour un fil de nylon de 0,3mm n = 3 donc n²= 3 × 3 = 9. La rupture à lieu pour une traction de 9 × 780 = 7020gr soit environ 7kg. Si on le tend avec 5,6kg (les 4/5e de 7kg) on se retrouve dans les conditions du fil de 8 centième ci-dessus soit un creux de 2,2mm sur une longueur de 50m.
NB: On peut définir une sorte d'indice de performance pour un matériau donné. Par exemple, pour le nylon, le creux à la limite de rupture est proche de 8mm pour 100m de distance. A partir de là, il est facile de calculer le creux pour n'importe quelle distance. Pour une distance n fois plus faible, le creux sera n2 fois plus faible.
Et si ça creuse trop en fin de compte ?
Si on peut placer un relais à mi-distance, surélevant le fil de la hauteur calculée, le fil creusera deux fois mais d'une hauteur 4 fois moindre.
Peut-on éviter tous ces calculs ?
Bien sûr que oui. Leur intérêt est surtout de savoir à l'avance à quoi il faut s'attendre. On peut toujours évaluer le creux par une simple visée en plaçant une règle à mi-distance.
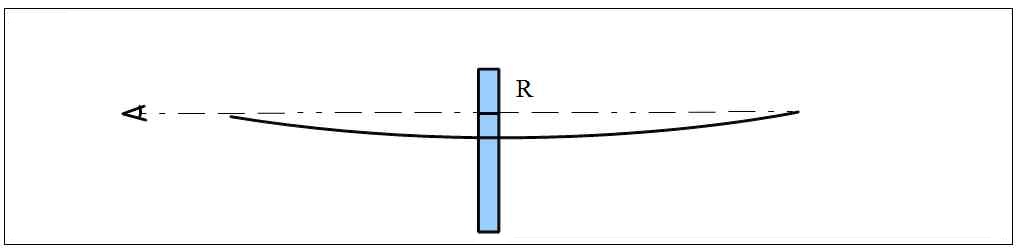
On aligne le repère R sur la ligne de visée. Le creux est donné par la distance entre le repère et le fil.
Mais au fait, si c'est pour faire un alignement, pourquoi ne pas utiliser un laser ? Disons que chacun a ses avantages et ses inconvénients .
Le coin des matheux
Les plus curieux se demanderons sans doute jusqu’à quel point on peut assimiler la fonction cosh(x) à une parabole. Voici la justification .
Aux valeurs proches de 0, la fonction ch(x) peut s’écrire sous la forme d’un développement limité :
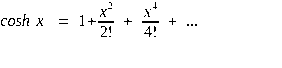
Rappelons que 2 ! = 1 × 2 = 2 et 4 ! = 1 × 2 × 3 × 4 = 24.
Le 1 au début de la formule ne fait que translater la courbe sans changer sa forme. On peut l’oublier !
Nous allons essayer quelques valeurs de x. Voyez le tableau ci-dessous.
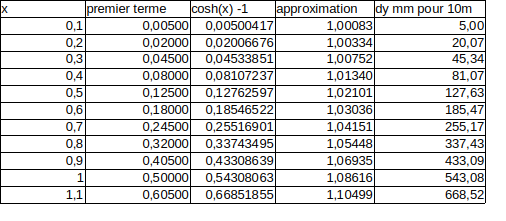
La quatrième colonne indique le ratio entre entre la valeur réelle de cosh (sans le terme 1) et l’approximation au premier terme.
La colonne suivante donne un cas concret : de combien ça creuse (en mm) pour une demie longueur de 10m.
On constate que la fonction cosh a bon dos. Il faut pousser x jusqu’à 1,1 pour avoir une approximation de 10 % avec un seul terme. On n’est plus franchement au voisinage de 0 !
Conclusion : Avec un fil bien tendu comme dans les exemples donnés plus haut, la parabole est vraiment une excellente approximation de la fonction cosh.
***** © M Guignard *****

Comments powered by CComment