Rotations suivant deux axes

La question soulevée ici est la suivante : De quel angle a4 varie la direction d’un objet qui subit deux rotations : une première d’un angle a1 suivant un axe x puis une seconde d’un angle a2 suivant un axe y, l’angle entre les deux axes étant a3.

La formule générale nous est donnée par la trigonométrie sphérique. On pourra consulter l’article de Wikipédia ici. Voici la formule :

Elle n’est pas particulièrement simple, d’autant qu’elle fait intervenir 3 variables.

Heureusement dans la majorité des cas les axes sont perpendiculaires, a3 = 90° ce qui nous donne cos(a3) = 0, et ceci  fait disparaître le second terme de l’addition. La formule devient :

Essayons avec deux angles de 45°:

Si l’un des angles vaut 90° (par exemple a1= 90°) son cosinus s’annule, l’équation s’annule. On obtient a4 = 90° quelque soit l’autre angle (a2 dans l’exemple).

Essayons d’imaginer ce qu’il se passe. Partons d’un plan horizontal, sa normale est verticale. On le fait pivoter de 90° suivant un axe horizontal orienté est-ouest. La normale se trouve alors horizontale, elle pointe au nord (et au sud). Si on fait tourner le plan suivant un axe vertical, la normale balaye l’horizon en restant constamment horizontale donc perpendiculaire à sa position d’origine.

Pour des angles quelconques, il n’est pas facile de prévoir le résultat final. Mais il est facile de faire un tableau à double entrée avec le tableur Calc ou son homologue bien connu de Microsoft ®.

Voici la formule dans la cellule B3 où a1 = a2 = 0 :

=ACOS(COS($A3*PI()/180)*COS(B$1*PI()/180))*180/PI()

Et voici le tableau complet après recopiage de la formule dans les autres cellules.

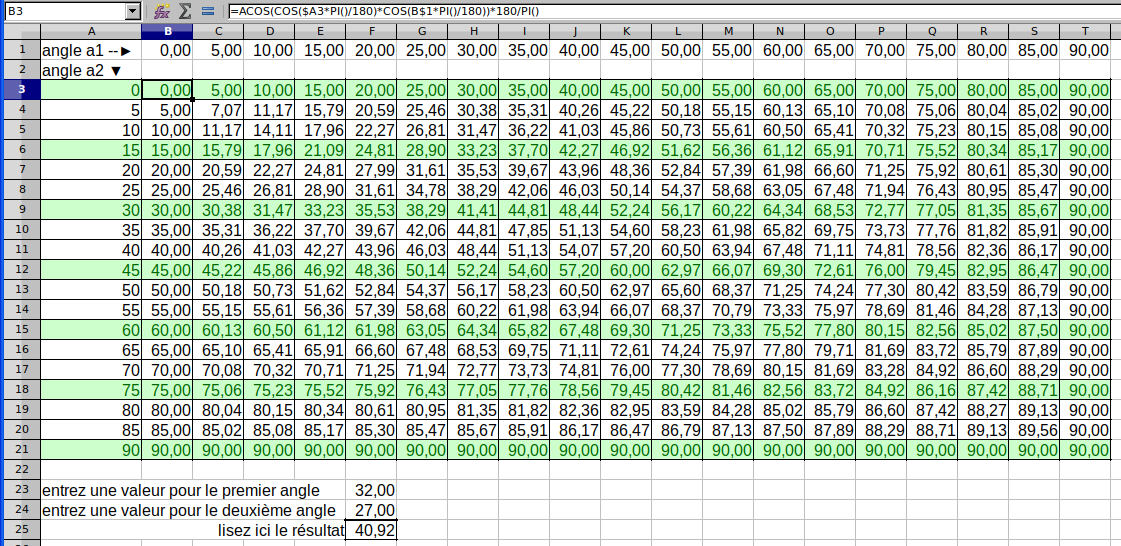
Ce tableau donne les valeurs de 5 en 5 degrés. Pour des angles intermédiaires on tapera les valeurs des angles ligne 23 et 24 comme indiqué et on lira le résultat en ligne 25 même colonne.

La formule en F25 s’écrit :

=ACOS(COS($F$23*PI()/180)*COS($F$24*PI()/180))*180/PI()

***** © M Guignard *****