volumes, poids, densités

Volumes, poids, densités

A-Masse volumique et densité

On appelle masse volumique d’un matériau sa masse par unité de volume. Par exemple, j’ai une pièce de fer de 10 cm x 5 cm x 5 cm. Son volume est de 250 cm³ soit 0,25 dm³.

Je le pèse et je trouve 1,97kg. J’en déduit que la masse volumique du fer est de :

1,97 / 0,25 = 7,88 kg/dm³.

On appelle densité le ratio entre la masse volumique d’un corps et celle de l’eau.

La densité de l’eau vaut 1 parce qu’on l’a voulu. Quand il a fallu définir une unité de masse, on a décidé de prendre une matière courante : l’eau et on a dit « l’unité de masse est la masse d’une unité de volume d’eau ». On aurait dû prendre le m³ comme unité de volume et on aurait eut la tonne comme unité de masse. Cette unité étant jugée trop grande et peu pratique, on s’en est tenu au dm³.

Définie comme ceci, la densité présente un aspect pratique intéressant : tout ce qui a une densité inférieure à 1 flotte dans l’eau (qui est tout de même le liquide le plus courant – avec ou sans jeu de mot –).

Vous trouverez ici

http://markuspopp.me/Table_des_masses_volumiques.pdf

une table assez complète des densités des matériaux.

J’ai souvent remarqué que beaucoup de personnes étaient fâchées avec les unité de volume. Voici donc quelques éclaircissements sur la question.

Le cm³ (prononcer centimètre cube) est le volume d’un cube de 1cm de côté.

Le dm³ (prononcer décimètre cube) est le volume d’un cube de 1dm de coté. 1dm = 10 cm.

Combien y a t’il de cm³ dans 1dm³ ?

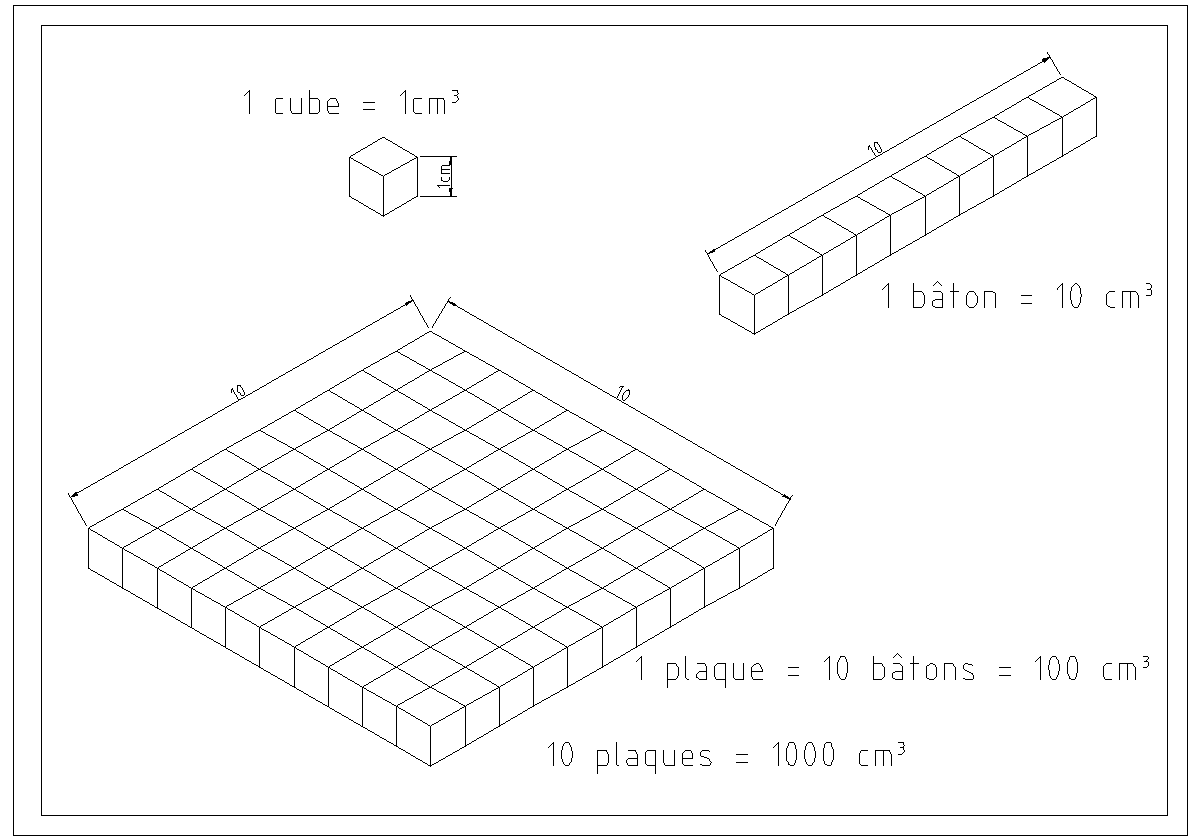
Supposons qu’on dispose de morceaux de sucre cubiques de 1cm de coté et d’une boite cubique de 10 cm de coté.

On peut faire des bâtons de 10 cm de long avec 10 sucres.

On peut faire des plaques de 10cm x 10 cm avec 10 bâtons soit 10 x 10 = 100 sucres.

On peut empiler 10 plaques dans notre boîte soit 10 x 100 = 1000 sucres.

Conclusion 1dm³ = 1000 cm³.

On prouverait de la même manière que 1m³ = 1000 dm³.

Mais on utilise aussi un autre vocabulaire. Vous n’achetez pas des bouteilles d’eau minérale de 1,5dm³ mais de 1,5 litres.

1litre = 1 dm³; 1m³ = 1000 litres.

Comme il y a 1000 cm³ dans 1litre, 1cm³ = 1 millième de litre on dit 1 millilitre.

Dans le milieu médical on abrège cm³ en cc (prononcer cécé).

1 dl (décilitre) correspond à 1 dixième de litre donc à 100 cm³.

1 cl (centilitre) correspond à 1 centième de litre donc à 10 cm³.

B-Masse et poids

Ce sont des notions parfois confondues.

La masse correspond à une quantité de matière. Comme la matière est essentiellement « remplie de vide », dans un même volume on peut avoir plus ou moins de matière. C’est pourquoi certains corps sont plus dense que d’autres.

La masse a 2 propriétés qui peuvent être utilisées pour la mesurer.

• En présence d’un champ gravitationnel, elle subit une force d’attraction : elle a un poids.

• Quand on essaie de l’accélérer elle résiste suivant la formule
                                       F = M x a.
  Il faut une force F d’autant plus élevée qu’on veut donner une accélération, a, forte et que la masse ,M, est importante.

On a l’habitude de mesurer les masses avec des balances qui mesurent leur poids. Comme la gravité est sensiblement la même partout sur terre cela ne pose pas de problème. Les 2 grandeurs sont liées par une constante g = 9,81 m / s² (valeur arrondie).

P = M x g.

Noter que si vous utilisez une balance à deux plateaux avec des poids calibrés, vous trouverez exactement le même résultat au pôle nord et à l’équateur, mais ce ne sera pas le cas si vous utilisez une balance à ressort ou à jauge de contrainte précise à quelques millièmes. Les choses seraient encore plus flagrantes sur la lune. On dit que les balances à poids calibrés comparent des masses ; les balances à ressort comparent des poids. Mais ceci n’est pas totalement vrai. Voir plus loin.

Jusqu’en 1948, on avait 2 unités qui s’appelaient kg.

• L’unité de masse était le kgm masse, la même que de nos jours.
• L’unité de force était le kgf = le poids d’une masse de 1 kg masse sur terre.

Ainsi la réponse à la question :  « Qu’est ce qui est plus lourd ? 1kg de plume ou 1kg de plomb. » était incontestablement : « Ils sont égaux», puisqu’on comparait deux poids.

Aujourd’hui la réponse est différente. Quand on pose cette question, on ne parle plus de poids de 1kg mais de masse de 1kg. Or le poids d’une masse donnée a deux composantes : la gravité qui s’exerce verticalement de haut en bas et la poussée d’Archimède qui s’exerce verticalement de haut en bas et donc réduit le poids..

Qu’est ce que la poussée d’Archimède vient faire ici ?

Rappelons son énoncé : Tout corps plongé dans un liquide reçoit de la part de celui-ci une poussée verticale dirigée de bas en haut égale au poids du volume de liquide déplacé.

Et corrigeons le : Tout corps plongé dans un liquide fluide reçoit de la part de celui-ci une poussée verticale dirigée de bas en haut égale au poids du volume de liquide fluide déplacé.

Ce qui est valable pour l’eau l’est pour l’air. Tous les objets qui nous entourent sont plongés dans l’air et subissent la poussée d’Archimède. C’est ce qui permet aux ballons gonflés à l’hélium de s’envoler. Oh, elle n’est pas bien importante, c’est pourquoi on la néglige quasiment tout le temps : 1,3 g /dm³.

Revenons à notre devinette. 1Kg de plomb a un volume plus petit qu’un kg de plume donc il subit une poussée d’Archimède plus faible, donc il pèse davantage. Attention cependant, la différence n’est pas aussi importante qu’on pourrait croire. Le volume à prendre en compte n’est pas celui du baluchon contenant les plumes mais le volume réel de la matière des plumes sans les vides entres les barbes.

Voici une expérience intéressante : Sur un plateau d’une balance précise, on place un récipient rempli de glace et on fait l’équilibre exact avec des poids et/ou du sable placé dans l’autre plateau. On attend que la glace fonde et on constate que la balance penche du coté de l’eau. Pourtant la masse s'est conservée et au pire si de l'eau s'était évaporée, la balance devrait pencher de l'autre côté.

En fait, la glace occupe un volume plus important que l’eau (c’est pourquoi les icebergs flottent) ; elle subit donc une poussée d’Archimède plus forte, elle est plus légère que la même masse d'eau. La masse de l’eau n’a pas changée mais son poids, si !

Attention, la variation est faible ! La différence de volume est de l’ordre de 10 %. Ainsi, 1kg de glace subit une variation de volume de 0,1dm³ donc une variation de poids de 0,13g.

Alors notre balance compare-t-elle vraiment des masses ou des poids ?..

On n’est pas complètement sorti de ce système des deux kg puisqu’on donne encore habituellement les poids en kg et les couples en kgm alors que l’unité de force officielle actuelle est le Newton.

Le Newton (symbole N) est la force qu’il faut appliquer à une masse unité (donc un kg) pour lui communiquer une accélération unité soit 1m/s² c’est à dire que sa vitesse augment de 1m/s à chaque seconde. On a ainsi un système d’unité cohérent.

1 kgf = 9,806 65 N ;

1 N = 0,101 972 kgf.

Souvent on nous parle de daN (déca Newton ) soit 10 N. C’est une façon astucieuse de ne pas trop nous perturber 1kgf est proche d’un daN.

Dans l’espace, loin de toute étoile ou planète, la gravité est quasi nulle les deux types de balances sont inopérantes et la seule manière de mesurer une masse est de la soumettre à une force connue et de mesurer son accélération ou l'inverse, par exemple en la faisant tourner au bout d’un ressort.

B.1-Calcul de volumes

Pour un parallélépipède rectangle, nommé maintenant ''pavé'' pour ne pas fatiguer nos fragiles écoliers d'aujourd'hui, le calcul est facile

V = l x p x h .

Il suffit de penser aux petits morceaux de sucre ci-dessus.

Pour un cylindre, on multiplie la surface de la base (le cercle soit πx R²) par la hauteur. Ben oui, si vous avez réussi à mettre d’une manière ou d’une autre, n morceaux de sucre sur une couche, comme vous ferez h couches, vous mettrez n x h sucres et ça marche si n et h ne sont pas entiers.

Pour un cône, c’est plus compliqué. On peut faire une approximation en empilant des rondelles cylindriques de plus en plus petites. Plus le nombre de rondelles est grand, plus l’approximation est bonne. Les mathématiciens savent empiler un nombre infini de rondelles (on appelle ça une intégrale) ce qui donne la valeur exacte :

V = 1/3 x s x h.

Le tiers du volume du cylindre de même base et même hauteur.

En fait, la formule est bien plus générale, elle s’applique aux pyramides de base quelconque : carrée, rectangulaire, polygone régulier à n coté. À ce titre, un cercle peut être considéré comme un polygone régulier ayant un nombre infini de cotés.

Pour une sphère, il faut aussi calculer une intégrale. On obtient :

V = 4/3 x π x R³.

Pour une calotte sphérique :

V= π h² /3 x (3 x R -h)

Vous trouverez d’autres formules concernant les aires et les volumes ici (entre autres):

http://www.volumeaire.com/volume-sphere.html

La surface du cercle est connue : S = π x R².

Je ne résiste pas au plaisir de vous présenter cette démonstration attribuée (à tord ou à raison?) à Archimède, que je trouve particulièrement simple et astucieuse. Voyez la figure ci-dessous.

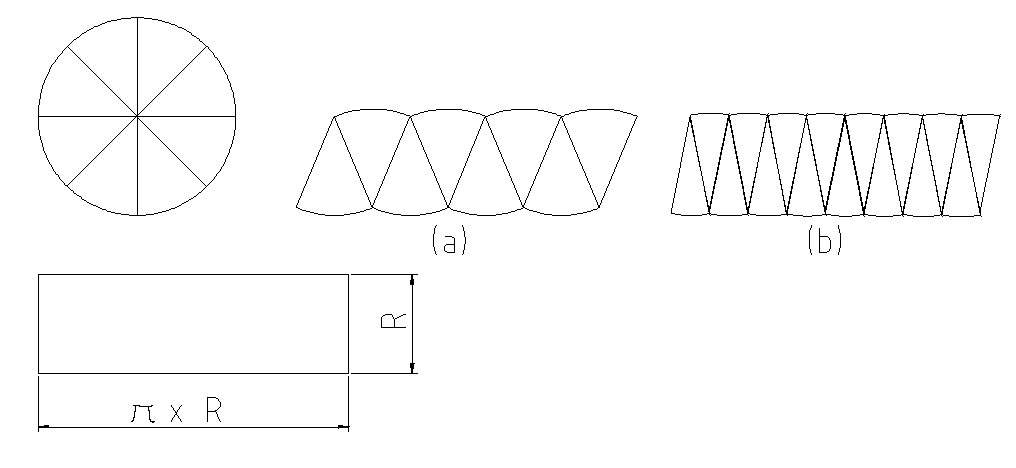
On a donc un cercle de rayon R. On le partage en 8 (par exemple) comme un gâteau et on imbrique les parts comme indiqué en (a). Il est facile de montrer que les parts s'emboîtent exactement. On obtient une figure avec 4 ondulations dont la longueur est celle de la demi-circonférence π x R et deux droites parallèles de longueur R, le rayon du cercle. Évidemment la figure a même aire que le cercle.

On coupe chaque part en 2 (ou plus) et on réassemble (figure b) et on recommence indéfiniment. À chaque fois les ondulations s’atténuent et les droites se redressent. La figure vers laquelle on tend est un rectangle de longueur π x R et de largeur R donc de surface S = π x R². C’est la surface de notre cercle.

 ***** © M Guignard *****