influence des approximations de mise en station
Le débutant en astronomie ne manquera pas de se poser la question suivante : Quel est l'effet d'une approximation de mise en station ; pour une erreur e donnée quelle est la dérive du champ observé?
La réponse courte est ± e . Cela signifie que pour une étoile donnée, il existe deux instants dans la journée où l'astre se trouve centré en affichant exactement sa déclinaison théorique. Aux autres horaires, la correction de déclinaison se situera entre + e et –e .
La figure 2 permet de comprendre ce qu'il se passe sans grands calculs. Elle est bâtie sur quelques points particuliers de la sphère céleste situés dans un même plan.
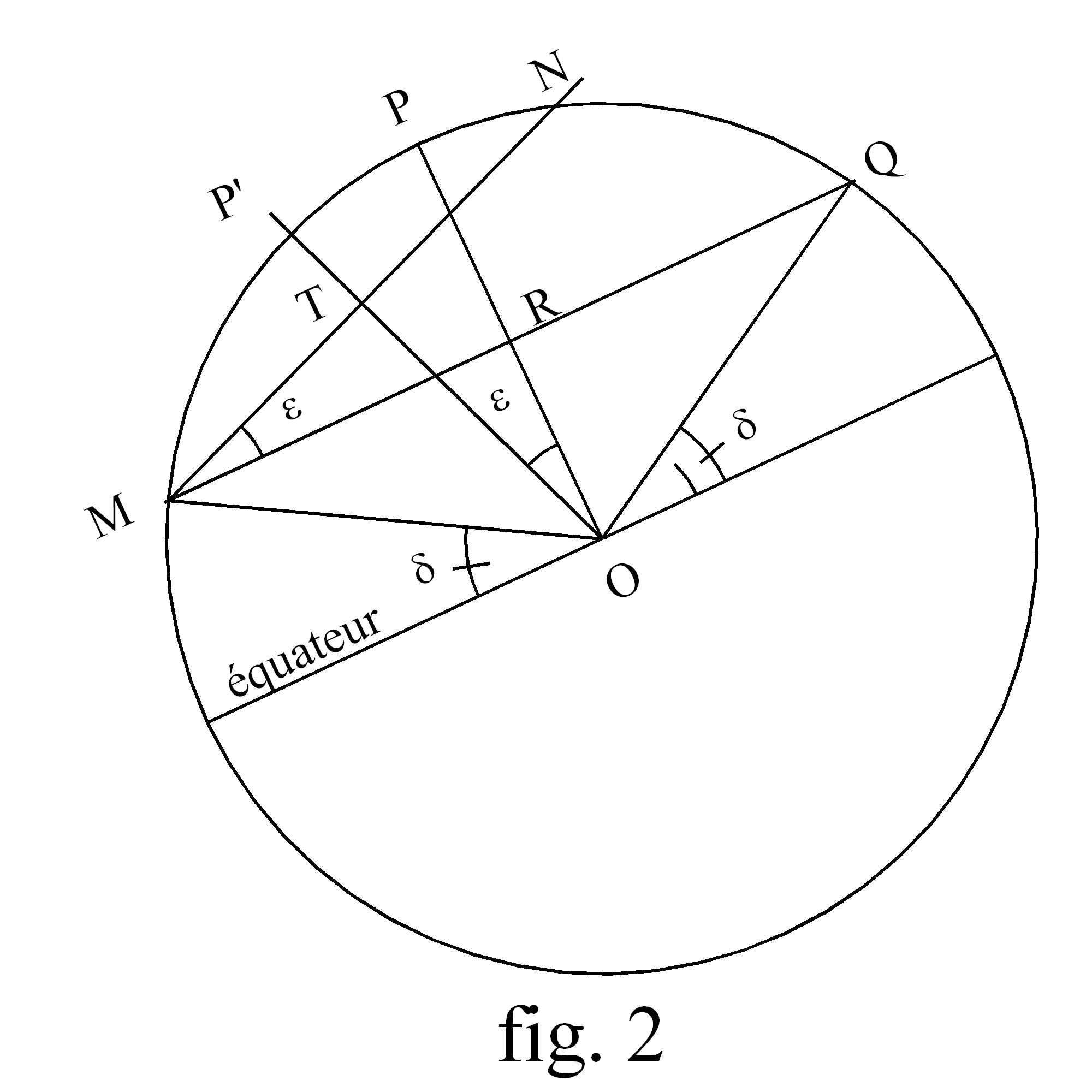
P est le PNC, P' est le point visé par l'axe polaire, O est le point d'observation. La figure représente le grand cercle de la sphère céleste qui contient P et P'. On considère une étoile E qui à l'instant t = 0 est située en M. Puisqu'elle décrit un cercle dont le centre R est sur l'axe des pôles, dans 12h4 elle sera en Q. La ligne MQ représente le cercle parcouru vu par la tranche. La droite MQ est un diamètre de ce cercle, R est dans le plan de la figure. Au départ le champ est centré sur M.
Cependant, l'axe polaire étant dans la direction OP', le centre du champ décrit un autre cercle dont MN est un diamètre et T le centre. Des considérations géométriques élémentaires nous permettent de dire que si l'arc PP' = e alors l'angle NMQ = e et l'arc NQ = 2e.
Ainsi, au bout de 12h, le centre du champ est en N alors qu'il devrait être en Q. Pour recentrer l'image on devra modifier la déclinaison de 2e.
L'angle POM représente le complément de la déclinaison d et P'OM le complément de la déclinaison affichée. On voit donc qu'à l'instant 0, la déclinaison a dû être réglée sur d + e. Douze heures plus tard il faut la mettre à d – e . Si on veut suivre l'étoile, il faudra bien dérégler progressivement la déclinaison sur une plage de 2e.
Ajoutons que cette dérive en déclinaison suit une loi quasi sinusoïdale. En M et Q, donc aux instant t = 0 et t = 12h la dérive est maximale mais sa vitesse est nulle ; aux instants t = 6h et 18h c'est l'inverse, la dérive est nulle mais sa vitesse est maximale. La vitesse maximale a pour valeur:
dmax = e / 60 par degré de champ parcouru.
Ce résulta a une valeur pratique importante. Supposons que l'on souhaite atteindre une galaxie peu visible en partant d'une étoile connue et en travaillant sur la différence des coordonnées . Pour une différence des AD de d mn la dérive sera inférieure à
e . d / 240 °
Par exemple, si la différence des AD est de 1h et l'erreur de m.e.s. de ½°, la dérive de l'une à l'autre sera inférieure à e / 4 = 1 / 8°. .
IL faut souligner que l'erreur en déclinaison s'accompagne d'une erreur en AD. Ainsi, même en corrigeant la déclinaison au fur et à mesure, on n'obtiendrait pas un recentrage parfait du champ avec un entraînement de l'axe polaire à vitesse constante. Pour s'en convaincre, il suffit d'examiner la situation à t = 6h. L'étoile ayant tourné d'un quart de tour, elle se trouve en un point R' sur la perpendiculaire au plan de la figure issue de R, tandis que le centre du champ est en T' sur la perpendiculaire issue de T. On voit bien qu'en le replaçant sur le cercle de centre R, on n'atterrira pas au niveau de R'.
Nous avons raisonné jusqu'ici avec une étoile dans une position particulière à l'instant 0. Tout ce qui a été dit reste valable pour une étoile quelconque ; il suffit de décaler l'origine des temps.
Une autre façon d'aborder le problème des dérives est de considérer un observateur situé au pôle nord. Il peut alors simplement suivre les étoiles avec une monture azimutale en bloquant la hauteur, car elles décrivent des cercles horizontaux. Si ensuite notre astronome se déplace suivant un méridien jusqu'à parcourir un arc e sur la sphère terrestre, il voit les cercles des étoiles s'incliner en se relevant coté sud. Il trouvera les astres à la bonne hauteur quand ils seront à l'est ou à l'ouest et les verra dériver dans son instrument au fil du temps. La dérive maximum e sera atteinte au nord vers le bas et au sud vers le haut.
Ajoutons que l'erreur de mise en station n'est pas la seule à intervenir dans un pointage aux coordonnées. Les erreurs de construction de la monture peuvent jouer un rôle non négligeable ainsi que les incertitudes de lecture, surtout sur les petites montures des télescopes de débutants style 115 x 900.
Contrairement à ce qu'on lit souvent, le pointage aux coordonnées est tout à fait possible avec une monture azimutale et il est même souvent beaucoup plus précis dans le cas des Dobson. Voir cet article.
***** © M Guignard *****
1) Voilà le genre d'explication que j'aurais aimé trouver dans la notice de mon télescope 115 x 900 quand j'ai débuté en astronomie.
Que de doutes levés en quelques lignes !
2) Pour savoir quelles graduations vous devez utiliser, procédez ainsi : Faites une mise en station grossière.
Pointez grosso modo vers l'horizon est. Maintenant tournez l'axe d'AD pour monter dans le ciel. Les graduations qui vous concernent
sont celles qui diminuent.
3) Mesure du champ d'un oculaire: voir l'article ici..
4) En réalité un peu moins. C'est la durée du jour sidéral qui compte ici. Par commodité on supposera qu'il dure 24h.

Comments powered by CComment