Pointage aux coordonnées avec un Dobson

Le pointage aux coordonnées, est impossible avec un Dobson. C’est du moins ce qu’on vous dira généralement. En fait, la phrase devrait être rectifiée ainsi : Le pointage aux coordonnées équatoriales, est impossible avec un Dobson. Par contre, non seulement il est tout à fait possible de pointer aux coordonnées azimutales, mais les Dobsons s’y prêtent particulièrement bien, comme nous allons le voir.

Pointing at coordinates is impossible with a Dobson. At least that's what you'll usually be told. In fact, the sentence should be corrected as follows: Pointing at equatorial coordinates is impossible with a Dobson. On the other hand, not only is it quite possible to point at azimuthal coordinates, but the Dobsons are particularly suitable, as we will see. 

pdf version here ---> ICI

A -Les coordonnées azimutales : un épouvantail ?

Si vous ne savez pas ce que sont les coordonnées azimutales et équatoriales, je vous invite à consulter cet article.

C’est bien connu, les coordonnées azimutales changent avec le lieu, le jour et l’heure. Dans ces conditions, il semble impossible de les utiliser couramment. C’est sans conter avec les progrès de la technologie. Ce qui demandait hier des calculs longs et fastidieux peut aujourd’hui être obtenu instantanément avec un ordinateur ou même une simple calculette programmable de type lycée.

A.I -Avec une calculette

Si on observe toujours du même endroit, ses coordonnées, longitude et latitude pourront être incluses définitivement dans le programme. Sinon, il faudra les entrer, une seule fois, au lancement du programme. Pour pointer un objet on donnera ses coordonnées équatoriales et l’heure exacte en TU. Si on repointe le même objet un peu plus tard, il suffira de donner uniquement la nouvelle heure. Tout cela se fait en moins d’une minute et le calcul est quasi instantané. Le passage des coordonnées équatoriales aux coordonnées azimutales si changeantes n’est donc pas un véritable obstacle. De plus, quand on compare les deux systèmes, il ne faut pas oublier qu’avec les coordonnées équatoriales, les ascensions droites doivent être constamment recalées si on ne dispose pas d’un moteur de suivi. Le recalage sur une étoile voisine, avant le pointage aux coordonnées, prend bien plus de temps que le calcul des coordonnées azimutales. Notez d'autre part, que ce recalage s’avère parfois nécessaire, même avec une motorisation, si la mise en station n’est pas parfaite.

A.II -Avec un ordinateur

Si on dispose d’un ordinateur sur le terrain, les choses sont encore plus simples.

Je raisonne ici avec l’utilisation du logiciel « Cartes du Ciel » mais d’autres conviennent également.

On lance donc cette application et on affiche la zone du ciel qui nous intéresse. Il suffit de cliquer à droite, sur l’objet à atteindre, pour en avoir toutes les informations, dont les coordonnées des deux types. Il n’est pas nécessaire de rentrer l’heure, le logiciel utilise celle du système.

Petite suggestion : On peut tricher soit sur l’heure, soit sur la longitude de manière à voir s’afficher les coordonnées azimutales de l’instant T + 1mn. Cette minute de décalage tient compte du temps nécessaire pour effectuer le pointage. Dans Cartes du ciel, le plus simple est de tricher sur la longitude qui doit être augmentée d’un quart de degré (15’) si c’est une longitude Est et diminuée d’autant si c’est une longitude Ouest.

Avec Stellarium, les choses sont encore plus simples puisque les coordonnées sont mises à jour en temps réel.

B -Afficher les coordonnées

Fort bien, me dira-t-on, mais ces fameuses coordonnées ne sont en général pas affichées sur les Dobsons. C’est vrai, il va falloir bricoler un peu, mais il n’y a rien d’insurmontable rassurez-vous. Ce texte est long parce qu’il est détaillé et que je propose plusieurs solutions à chaque étape.

Il y a trois choses à faire.

• Un plateau d’horizontalité.

• Des graduations en azimut de 0 à 359°.

• Des graduations en hauteur de 0 à 90°.

B.I -Le plateau

Pour que les mouvements des deux axes soient totalement découplés, il faut que l’ensemble repose sur une base parfaitement horizontale. Toutefois on verra au dernier paragraphe qu’une inclinaison légère n’est pas vraiment catastrophique.

Si le sol est dur, comme une dalle ou des pavés autobloquants, le problème sera solutionné simplement avec un plateau en aggloméré muni de 3 pieds réglables avec des vis.

Si le sol est meuble, comme une pelouse, les choses sont un peu plus compliquées. On pourra par exemple interposer des pavés de ciment entre le sol et les pieds du plateau.

En fait, il est préférable d'avoir 1 pied fixe. En effet si vous agissez sur les 3 pieds vous risquez de dériver petit à petit et de vous retrouver avec un pied bloqué tout en haut ou tout en bas.
Voici une bonne méthode:
supposons pour faciliter les explications que les 2 pieds réglables soient orientés suivant une ligne est-ouest.
-- Vous placez votre niveau suivant une direction perpendiculaire donc nord-sud et vous faites monter ou descendre les 2 pieds réglables simultanément d'une même quantité dans le même sens. Votre plateau pivote suivant un axe est-ouest jusqu'à ce que le niveau indique l'horizontalité.
-- Vous placez votre niveau suivant la direction perpendiculaire à la précédente, donc est-ouest dans mon exemple et vous faites monter ou descendre les 2 pieds réglables simultanément d'une même quantité mais en sens inverse. Votre plateau pivote suivant un axe perpendiculaire au niveau jusqu'à ce que le niveau indique l'horizontalité.
Votre plateau est alors parfaitement horizontal si vous avez bien agit en quantités égales sur les pieds réglables.
Faites un second tour au besoin.

B.II -Les graduations d’azimut

Ce sont les plus longues à faire. Je donne plusieurs solutions.

B.II.a -Pour les bricoleurs paresseux

Ceux qui veulent bricoler un minimum pourrons se contenter d’enrouler un mètre de couturière autour du rocker, sur la tranche. Scotcher d’abord l’extrémité avec la graduations maximale (150 cm souvent, insuffisant pour un rocker de 50cm, mais on trouve aussi des 3m). Enrouler en tendant bien et scotcher l’extrémité 0. Il y a deux possibilités : placer le mètre sur le plateau fixe, ou sur le rocker qui tourne au-dessus.

• Dans le premier cas, l’index sera placé sur le rocker. Le mètre doit être enroulé dans le sens inverse des aiguilles d’une montre (la graduation 10cm est à gauche du 0).

• Dans le second cas, l’index sera posé sur le plateau d’horizontalité. Le mètre doit être enroulé dans le sens des aiguilles d’une montre (la graduation 10cm est à droite du 0).

Avec cette méthode, les indications ne correspondent pas à des degrés ; un coefficient de conversion k doit être appliqué. On a :

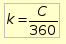
où C est la circonférence du rocker, la valeur lue sur le mètre de couturière au niveau de l’extrémité 0.

NB :Si k et C sont exprimés en mm, k correspond à l’espace d’un degré en mm.

Pour faire la conversion, on a plusieurs possibilités.

• Utiliser une calculette. La valeur de k étant entrée en mémoire, il n’y a plus qu’à faire (valeur azimut) x [MR ] (rappel : [MR] = touche de rappel de la valeur en mémoire), pour obtenir la valeur à lire en mm.
  EX : Le rocker fait 50 cm de diamètre. On va trouver C= 1570mm et k =4,3633... Si l’azimut à atteindre est 28°15’ la valeur à lire sur le mètre sera :  28,25 × k =123,26mm.
  Si les coordonnées sont obtenues par un programme sur calculette, la conversion pourra être directement incorporée au programme !

• Utiliser une table de conversion. Cette table sera établie à l’aide d’un tableur. En principe, elle doit avoir 360 valeurs, ce qui peut sembler beaucoup. Une solution serait de n’inscrire que les valeurs paires, 180 valeurs, ça devient plus raisonnable. On obtient la valeur impaire suivante en ajoutant k mm.

On peut même se limiter à 36 valeurs de la façon suivante :

On ne note que les valeurs d’angles multiples de 10°. Par contre l’index comporte non pas un seul trait mais dix espacés de k mm et gradués de 0 à 10. Si on veut par exemple régler l’azimut sur 16°, on placera la graduation du mètre correspondant à 10° sur la graduation 6 de l’index.

B.II.b -Pour les bricoleurs un peu plus courageux

Voici deux méthodes pour mettre en place une véritable graduation en degrés.

B.II.b.i Graduations sur la tranche

Au lieu du mètre de couturière (voir en B.II.a), on enroule un bout de sangle de couleur unie claire.

On fait une marque là où l'extrémité libre vient recouvrir l'extrémité scotchée. On déroule, on mesure C.

On calcule D = C / 36. D est l'interval correspondant à 10°.

On calcule à l'aide d'un tableur (Excell ou Calc) les 35 premiers multiples de D. On place un mètre à ruban parallèlement à  la sangle, le zéro en face de l'extrémité de début (attention au sens voir le premier paragraphe en B.II.a) et on reporte soigneusement les 35 valeurs  calculées sur la sangle et on écrit les valeurs d'angles multiples de 10°.

On remet en place la sangle sur la tranche du rocker ou du plateau fixe. On réalise un index couvrant 10°(figure ci-dessus). Et le tour est joué!

NB: Pour un index posé sur le plateau, les graduations de la figure ci-dessus sont à inverser.

B.II.b.ii Graduations à plat

Les graduations seront ici mises à plat sur le rocker. On commence, comme en B.II.a, en plaçant un mètre de couturière sur la tranche du rocker.

De la valeur de C, lue sur le mètre, on déduit le rayon du rocker. Comme on ne pourra pas imprimer la couronne d’un seul tenant, on va décomposer celle-ci en arcs qui seront placés ensuite bout à bout. Chaque arc couvrira 60°. Cette valeur convient pour un rocker de 50cm de diamètre voire un peu plus et une impression en paysage A4. Le dessin est fourni figure1, il suffit de l’imprimer en adaptant l’échelle. Vérifier avec les cotations.
Petite astuce : On démarre le premier arc sur la graduation 5° au lieu de 0 pour ne pas avoir à inscrire des valeurs aux extrémités à cheval sur deux arcs.
Après impression, de préférence sur du bristol, on découpera les différentes pièces. Pour les coller sur le rocker, on s’alignera sur les indications du mètre de couturière : la graduation 0 en face du 0, la graduation 60° en face de C/6 etc.. L’index pourra être une arête verticale d’un cube de bois ou d’autre matière plus lourde. Voir plus loin comment placer l’index au bon endroit. Si on a une préférence pour la position de l’index, il faudra y songer dès le départ, au moment de la mise en place du mètre de couturière. Dès que les 6 pièces de bristol sont collées, à leur place très précise, le mètre peut être retiré.

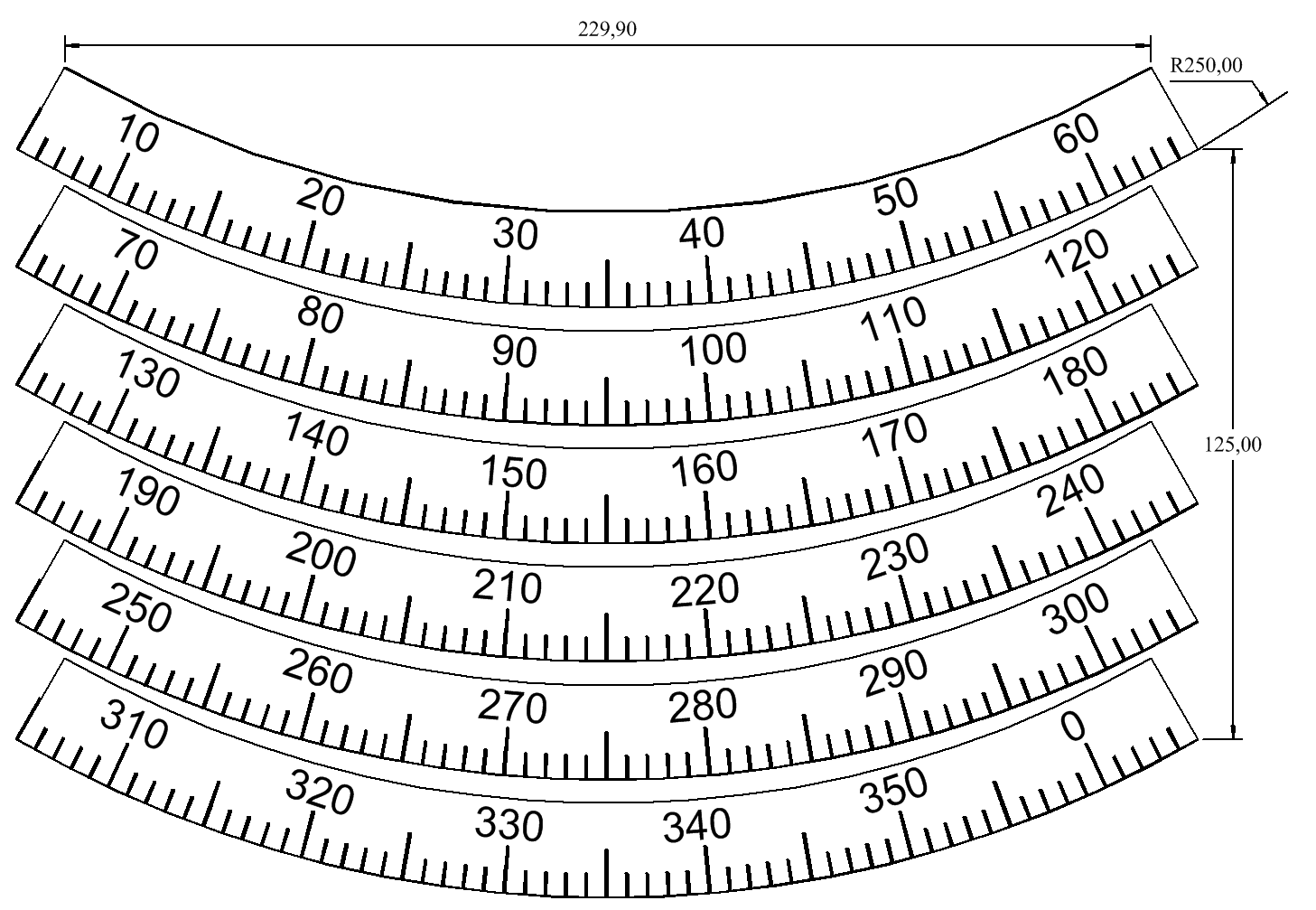
figure 1 Faire clic-d dans l'image pour accéder à l'image à l'échelle 1

B.II.c La solution électronique

La voie royale consiste à afficher les angles avec des afficheurs 7 segments à leds rouges. On peut alors lire les angles sans lampe et sans éblouissement. Un tel dispositif est trop complexe pour être entièrement décrit ici. Le principe consiste à compter des impulsions fournis par des fourches optoélectroniques entre les branches desquelles défilent des zones alternativement opaques et transparentes quand le rocker tourne.

B.II.d Graduations sur une fraction de cercle

Au lieu de travailler sur les valeurs absolues des azimuts, on peut se contenter d'utiliser des valeurs relatives. Un objet à observer est toujours relativement proche d'une étoile parfaitement identifiable. Dès lors, il suffit de pouvoir mesurer le petit angle qui les sépare en azimut. Tout cela, et la réalisation des plus simples qui va avec, est expliqué dans un autre article tout à la fin.

B.III -Les graduations de hauteur

Pour mesurer l’angle de hauteur, on va utiliser une sorte de fil à plomb se déplaçant sur un quart de cercle gradué (figure 2).

La mesure se fait en posant le côté AB de la planche sur la ligne de crête du tube.

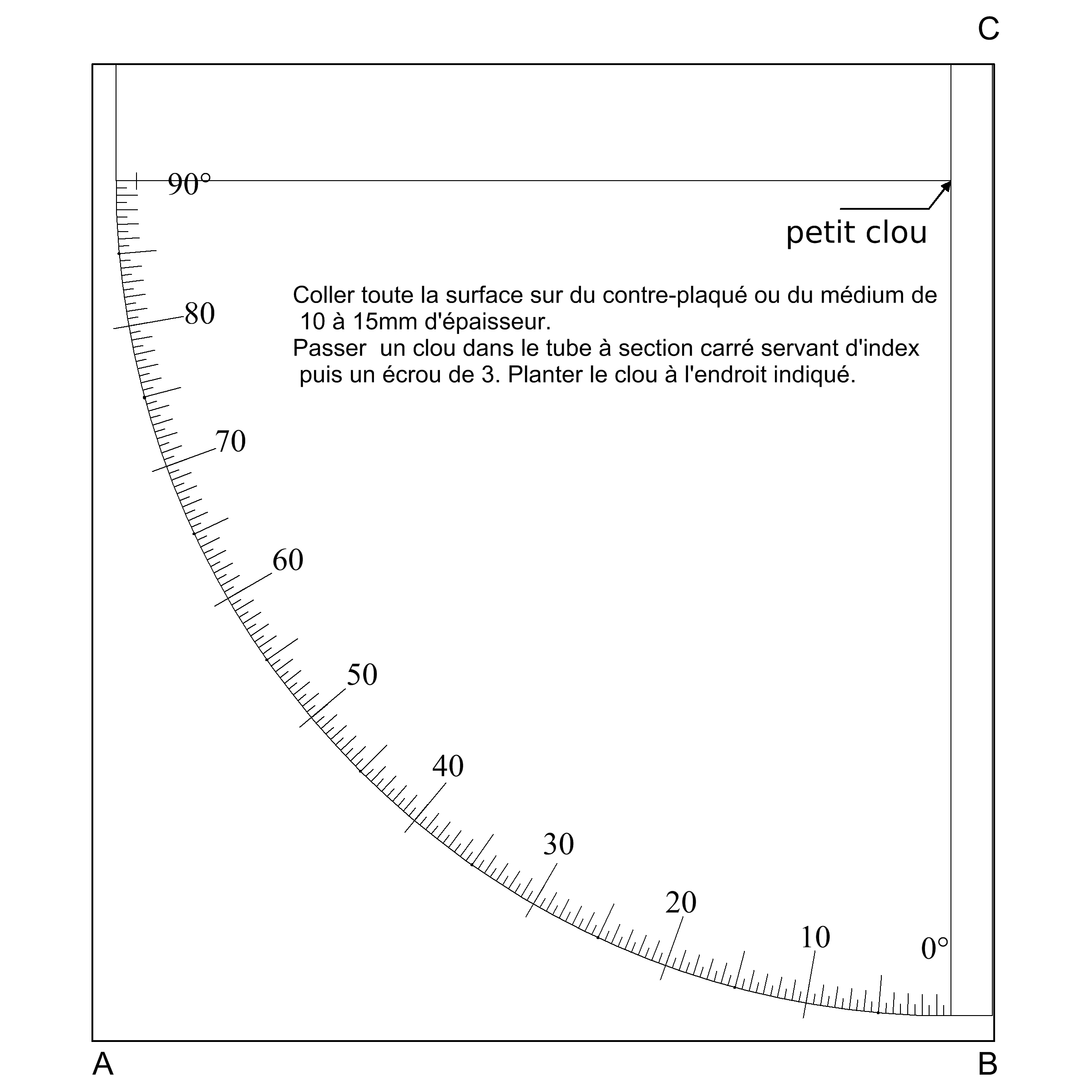
figure 2 Faire clic-d dans l'image pour accéder à l'image à l'échelle 1

L’index (le « fil » à plomb) est réalisé avec un tube à section carré en aluminium percé de part en part d’un petit trou permettant le passage d’un clou, vers une extrémité. Le tube est lesté par une barre de fer de quelques cm de long vers l’autre extrémité. Cette extrémité est sciée en pointe. C’est la pointe qui indique l’angle (figure 3).

figure 3

Mais vous pouvez aussi utiliser un inclinomètre du commerce qui vous coûtera une vingtaine d'euros.

C -Utilisation

Remarquons d’abord qu’on n’a pas fait tout ça pour rien. Utiliser nos graduations sera un vrai bonheur. On travaille sur de grands cercles, ce qui nous donne plusieurs mm par degré ; on peut ainsi raisonnablement espérer un placement au ¼ de degré près ou presque. Les conditions n’ont rien à voir avec celle des petites montures équatoriales où les cercles de l’ordre de 8 cm de diamètre ne laissent pas espérer une précision meilleure que 1,5 à 2°.

C.I -Les azimuts

La seule chose à faire préalablement, consiste à placer soigneusement l’index. Pour cela, il suffit de pointer une étoile bien identifiée, de demander au logiciel son azimut actuel et de placer l’index en conséquence.

C.II -Les hauteurs

Pour les hauteurs, c’est on ne peut plus simple. On pose la base de l’outil sur le dos du télescope et on lit directement la valeur indiquée par l’index.

Au premier essai, il faudra vérifier que les indications sont justes. Poser un niveau sur le dos du télescope et régler à l’horizontalité exacte. Bloquer la position. Poser l’instrument et vérifier qu’il indique 0°. Si ce n’est pas le cas, caler par en dessous ou retoucher la pointe du curseur.

D -Influence d’une erreur d’horizontalité du support

Le calcul de cette erreur est un peu complexe. J'y reviendrai une autre fois. Je ne donne ici que les conclusions.

La principale chose à retenir est que, l’erreur en hauteur étant annulée (puisque la mesure est indépendante de l'orientation du support), si on doit tâtonner pour trouver un objet, c'est uniquement en azimut. Et n'avoir à tatonner que dans une direction, ça change tout!

Remarquons d'autre part que la précision d’un niveau est habituellement de 2mm/m soit un angle de 0,11°. Il est donc tout à fait possible de rendre négligeable l’erreur d’horizontalité.

***** © M Guignard *****