Définir un cercle de 100 km de rayon

J'ai retiré de cet article les paragraphes A à D, au final, sans grand intérêt.

Voyez aussi  cet article à la fois plus concis et plus général:

comment tracer un cercle de rayon donné autour de chez soi

Mai 2020. Par ces temps de semi-confinement, on est autorisé à circuler en France dans un rayon de 100km à vol d’oiseau, autour de chez soit. Cet article vous propose deux solutions pour déterminer jusqu’où vous pouvez aller en traçant sur une carte un cercle de 100km de rayon centré sur votre lieu d’habitation.

May 2020. In these times of semi-confinement, one is allowed to travel in France within a radius of 100km as the crow flies, around one's home. This article proposes two solutions to determine how far you can go by drawing on a map a circle with a radius of 100km centered on your place of residence.

Cette méthode consiste à placer une série d’épingles délimitant le cercle de rayon 100km sur une Framacarte. La position des pins est importée sous la forme d’un texte issu d’un document Calc (ou Excel).

Voir en E-II pour un tableur tout prêt.

Faire la carte

Pour obtenir la bonne carte, je vous propose d’utiliser Framacarte.

Vous pourrez trouver ici les bases de l’utilisation de Framacarte :

https://framablog.org/2016/03/04/comment-creer-sa-premiere-framacarte-tutos-umap-24/

Débutez donc une nouvelle carte > À droite choisissez le fond de carte qui convient en cliquant sur la pile de feuille : Openstreetmap.fr. Faites des clic-gl jusqu’à placer votre lieu de résidence au centre de la carte. Zoomez fort avec les gros + et – en haut à gauche de façon à situer votre lieu de résidence.

Voilà, vous avez la carte qu’il vous faut.

E.I -Le calcul des positions

Nous allons placer une épingle tous les 10° soit 36 au total (plus une au centre). Je détaille ici la procédure de calcul, mais ceux qui n’aime pas les maths peuvent sauter ce paragraphe.

Le rayon de la terre est d’environ 6367km (moyenne entre le rayon équatorial et le rayon polaire). La circonférence est donc de 40008km et 1° correspond à 111,13km (40008/360). On en déduit que 100km correspondent à 0,9° à très peu près.

E.I.a -Première approche

Supposons que vous soyez au point de latitude 0° et longitude 0° donc sur l’équateur. On écrira 0;0. Appelons C ce point.

Si, depuis C :

• Vous faites 100km à l’est vous serez au point E 0° ; 0,9°. La direction de E est 0°.

• Vous faites 100km à l’ouest vous serez au point O 0° ; -0,9°. La direction de O est 180°

• Vous faites 100km au nord vous serez au point 0,9° ; 0°. Soit N ce point. De direction 90°.

• Vous faites 100km au sud vous serez au point -0,9° ; 0°. Soit S ce point. De direction 270°.

• Vous faites 100km dans une direction d comptée dans le sens trigonométrique avec CE comme origine. Vous êtes au point P de coordonnées 0,9 sin(d) ; 0,9 cos(d).

Supposons maintenant qu’on parte du point C1 de coordonnées 2°; 3°. Le point P1 se calcule en ajoutant les coordonnées de C1 soit 2+0,9sin(d) ; 3+0,9cos(d).

E.I.b -En France

Quittons les chaleurs équatoriales pour la France. Plaçons nous au point 47° ;6°. Il y a maintenant un problème supplémentaire : Le parallèle de latitude 47° a un rayon nettement plus petit que R0 celui de l’équateur. Il vaut R0 cos(47°).

Les coordonnées de P sont donc 47 + 0,9 sin(d) ; 6 + 0,9 /cos(47) .cos(d).

Mais nous avons fait une petite approximation : Ce n’est pas cos(47) qu’il fallait prendre en toute rigueur mais cos( la latitude de P).

Finalement, cas général  :

latitude P :         La = Lac + 0,9 sin(d)

longitude P :      Lo = Loc + 0,9 / cos(La) . cos (d)

où Lac et Loc sont respectivement la latitude et la longitude du centre, donc de votre lieu d’habitation.

E.II -Le tableur

Il est maintenant facile de faire un tableau des positions de 10° en 10°.

Toutefois vous trouverez un tableur tout fait  ici

Si vous voulez être autonome, démarrez un fichier Calc (ou Excel)

• La colonne A contient les angles de 0 à 350° de 10 en 10° (ou ce que vous préférez).

• La colonne B affiche les latitudes

• La colonne C affiche les longitudes

• Dans la cellule A1 écrivez angles °; en B1 latitude; C1 longitude ; en D1 Lac ; en E1 la valeur de votre latitude ; en D2 Loc ; en E2 la valeur de votre longitude.

• Écrivez 0 en A2 et 10 en A3 > sélectionnez A2 et A3 et tirez le petit carré vers le bas pour obtenir la suite 20, 30, 40… jusqu’à 350 inclus.

• Écrivez en B2 : =$E$1 + 0,9*sin(radians(A2))

• > tirez vers le bas jusqu’à la ligne 37

• Écrivez en C2 : =$E$2 + 0,9/cos(radians(b2))*cos(radians(A2)) > tirez vers le bas.

• Ligne 38 en B écrivez = $E$1 et en C =$E$2 .Ceci marquera le centre du cercle. En principe inutile voir remarque ci-dessous.

Votre tableur est prêt !

Remarque: Pour  trouver les coordonnées du centre, placez un marqueur puis cliquez dessus > clic sur le stylo > dans l'espace noir de droite descendez sur coordonnées: elles sont là avec une précision qui laisse rêveur. Gardez 4 décimales ce sera très largement suffisant. Les coordonnées en bas du tableur font donc double emploi.

Si vous avez un environnement français, le séparateur décimal est la virgule. Il nous faut remplacer ces virgules par des points :

Sélectionnez toutes les colonnes utilisées > clic-d > formater les cellules > onglet nombre > langue : choisissez anglais(USA). Vous pouvez en profiter pour limiter le nombre de décimales à 4 ; ce sera bien suffisant.

Enregistrez votre tableur.

Copiez le contenu des colonnes B et C > rendez-vous sur votre carte > Ajoutez un calque en cliquant sur la pile de disques à droite.> clic sur le + > appelez le cercle100km. > plus bas forme de l’icône : choisissez épingle > le reste se comprend facilement, je vous laisse faire. > fermer.

Clic sur la flèche montante au-dessus de la roue dentée > choisissez votre calque cercle100km (mais ça devrait être déjà fait) > format des données : csv > dans la petite fenêtre sous renseigner une URL faites [Ctrl] + [V] pour coller vos données. > clic sur importer et voyez le travail !

Pour faire une autre carte avec un autre cercle centré sur d’autres coordonnées, vous n’avez qu’à changer le contenu des cellules E1 et E2 et refaire une importation.

Voyez le résultat au complet et à l'échelle 5km.

NB: Faites clic-d (dans l'image) > afficher l'image pour obtenir la résolution native de l'image.

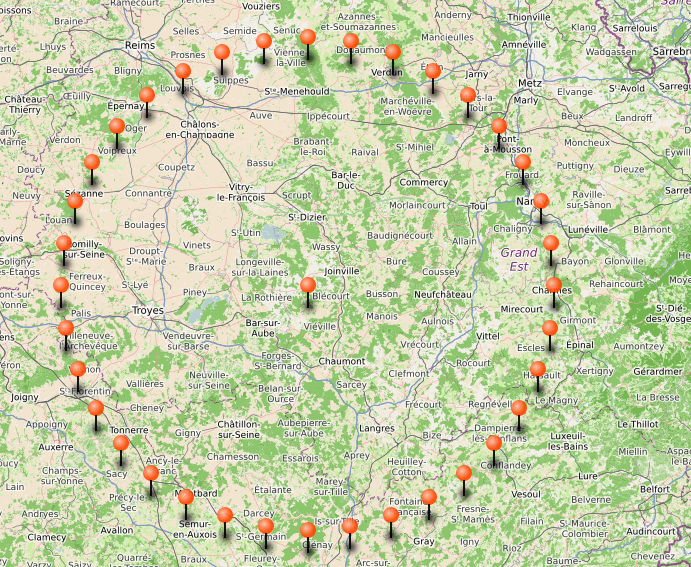
 une autre zoomable à souhait:

Voir en plein écran

***** © M Guignard *****