Comment faire une girouette sensible
Je vous propose ici de réaliser une girouette. Avant de passer à la construction, nous allons faire un peu de théorie pour voir ce qui doit guider la conception de notre girouette.
I propose here to make a weather vane. Before moving on to the construction, we will do a little theory to see what should guide the design of our weather vane.
NB: Pour voir les images parfaitement faites clic droite > afficher l'image
A - Un peu de théorie
Ce chapitre s’adresse à ceux qui n’ont pas les bases en mécanique et qui veulent apprendre.
Si ce paragraphe vous ennuie, vous pouvez le sauter, mais jetez un œil aux figures à partir de la 6.
En général, les amateurs de girouettes se posent peu de question sur la sensibilité de leurs réalisations. Pourtant qu’est ce que l’on veut ? Un instrument qui s’oriente de temps en temps sous les fortes bourrasques ou quelque chose de très sensible capable de réagir au moindre zéphyr ? Il me semble intéressant de savoir s’il est facile d’obtenir de bonnes performances et comment optimiser les différents paramètres entrant en ligne de compte.
Pour qu’une girouette tourne, elle doit être soumise à ce que les physiciens appellent le moment d’un couple (en langage courant on dit un couple) et il faut que celui-ci soit supérieur aux frottements. Pour qu’elle indique la direction du vent, le moment doit s’annuler quand elle atteint cette direction, mais rester suffisant quand elle en est proche.
A.I - qu’est ce qu’un couple ?
Pour faire simple, nous dirons qu’un couple est l’association de 2 forces parallèles de sens opposées, séparées par une certaine distance, comme sur la figure 1 (a).
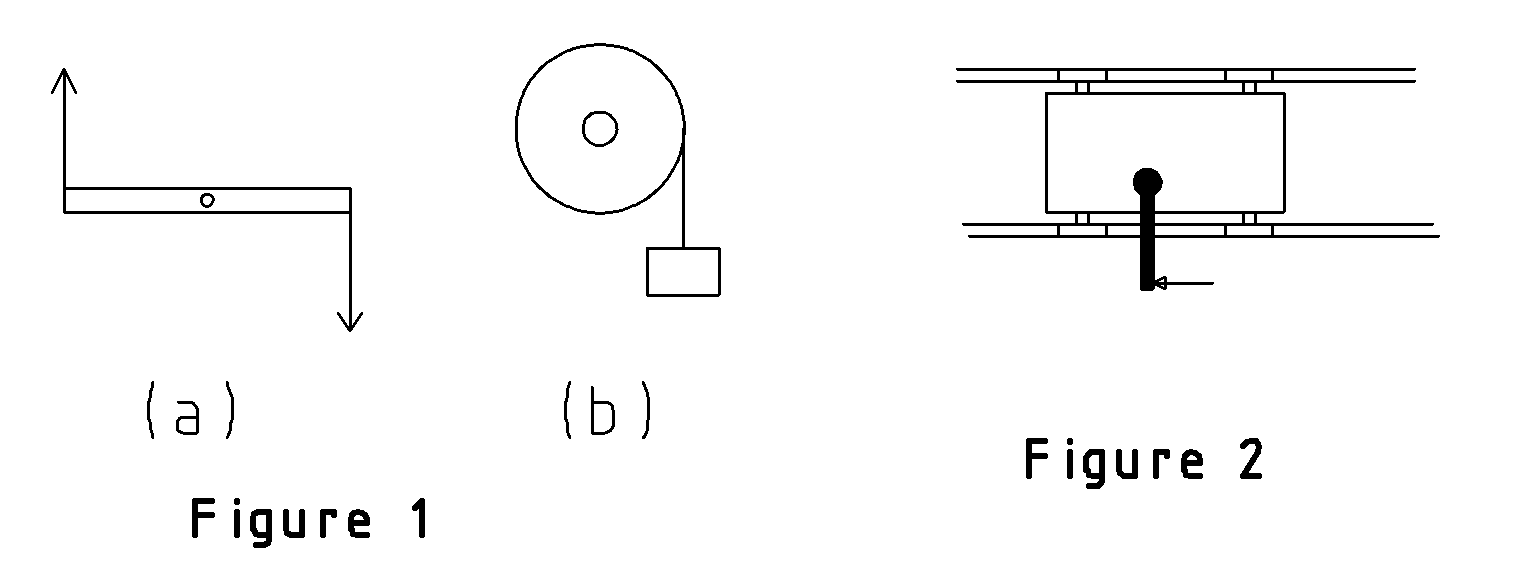
Toutefois, souvent, on ne voit qu’une force comme dans le cas de la figure 1(b) où une ficelle terminée par un poids est enroulée sur une poulie. En réalité, la seconde force est bien présente. Si la poulie tourne c’est parce que l’axe est soumis à une force, dite de réaction, qui l’empêche d’être entraînée par le poids.
Imaginez un chariot placé sur des rails (figure 2).
Ce chariot comporte un axe vertical autour duquel peut pivoter un bras perpendiculaire aux rails. Toutefois ce bras est freiné modérément en rotation. Si vous poussez sur le bras, celui-ci tend à tourner, mais en même temps, le chariot tend à avancer. Si la résistance à l’avancement est faible, votre bras ne tournera pas, le chariot avancera. Par contre, si vous freinez fortement le chariot, il restera sur place et le bras tournera.
A.II - Moment d’un couple
La grandeur physique qui fait tourner les objets est le moment du couple. C’est le produit d’une des 2 forces par la distance entre les deux, à condition que ces forces soient perpendiculaires au bras de rotation, sinon il faut considérer les composantes perpendiculaires(voir en A-III). Dans le cas de la poulie qui tourne c’est le produit du poids par le rayon de la poulie. Dans le cas d'une girouette c'est le produit de la force du vent par la distance à l'axe de la surface de prise au vent. Pour augmenter le couple, il faut augmenter la surface (on augmente la force) et la distance à l'axe.
Notez que par abus de langage on parle souvent de couple à la place de moment d’un couple.
A.III - Composantes d’une force
Une force peut toujours être considérée comme la somme de plusieurs composantes (et inversement). Souvent on s’arrange pour que les composantes soient perpendiculaires entre elles.
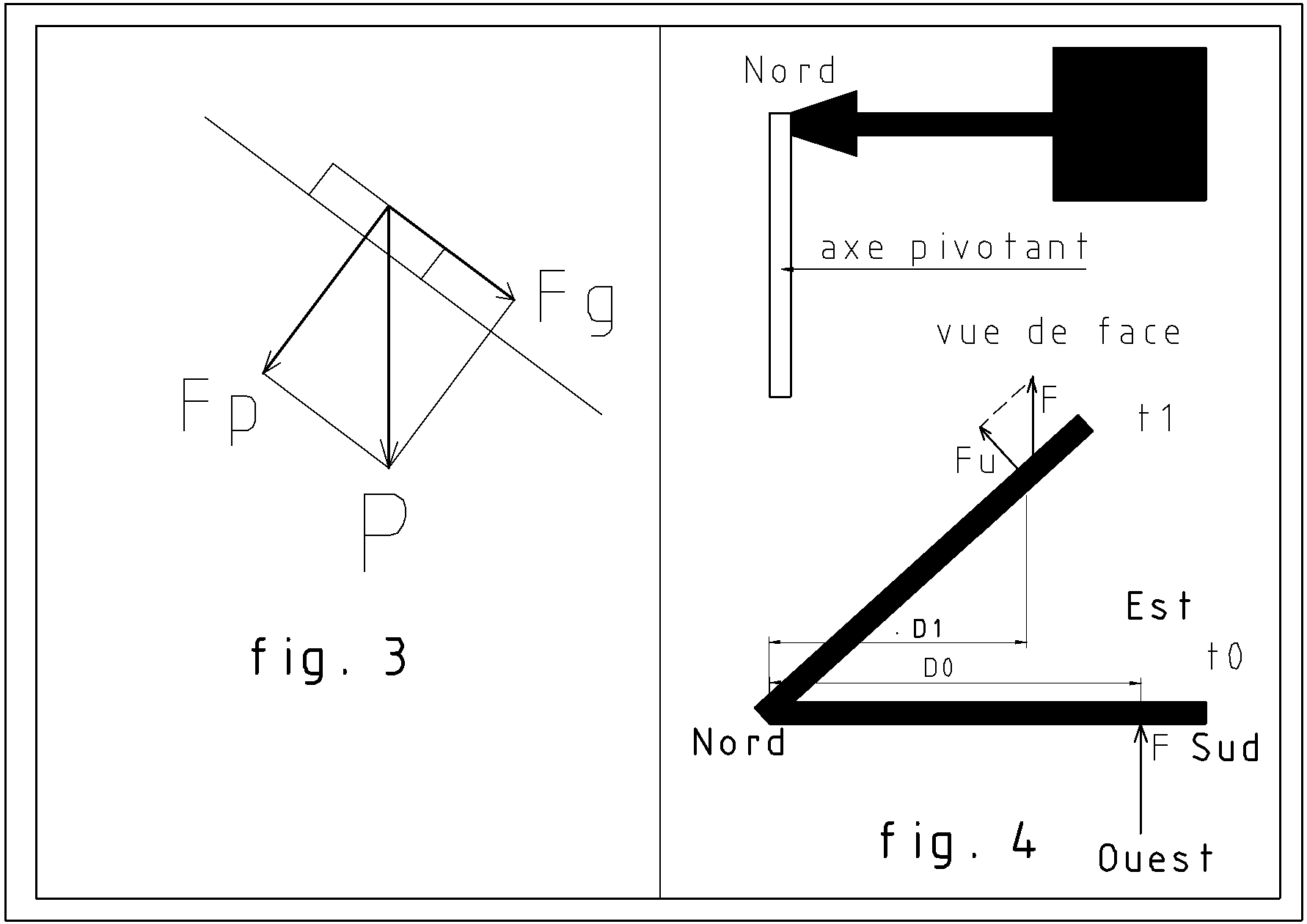
Considérons, figure 3, une objet sur un toit. Il est soumis à une force verticale : son poids. Cette force verticale peut être considérée comme la résultante d’une force fp qui plaque l’objet sur le toit et d’une force fg qui tend à la faire glisser sur le toit. Pour évaluer la valeur de chaque composante, il suffit de tracer une verticale proportionnelle au poids de l’objet (par exemple 1cm par N), puis la perpendiculaire au toit passant par l’extrémité de la ligne de poids et enfin la parallèle au toit passant par l’extrémité commune des 2 lignes précédentes. La longueur de chaque ligne représente la force correspondante avec le même coefficient de proportionnalité.
A.IV - Moment d’une girouette minimaliste
Imaginons une girouette minimaliste comme dessinée figure 4 en haut. Et représentée en vue de dessus en bas
À l’instant t0, la girouette pointe au nord et le vent souffle d’ouest en est. Une force F qui dépend de la vitesse du vent s’exerce perpendiculairement à la surface carrée et le moment du couple est égal à M0 = F × D0. La girouette commence à tourner.
À l’instant t1, la girouette pointe vers le nord-ouest. La distance entre la force du vent et l’axe est réduite. Elle vaut D1 = D0 × cos(45°) soit environ 0,7 D0. D’autre part, la partie utile de la force est la composante perpendiculaire à la tige soit Fu = F cos (45°) = 0,7 F.
En définitive, le moment s’est divisé par 2 sur une rotation de 45°( 1 / cos2(45°)).
Pour une rotation quelconque, le moment sera multiplié par cos2(a) où a est l’angle de rotation depuis la perpendiculaire au vent.
On comprend que pour a = 90°, soit une orientation parallèle au vent, le moment s’annule (cos(a)=0) et la girouette ne tourne plus. C’est bien l’effet recherché.
Par contre, pour a = 80° soit tout de même 10° avant la direction exacte, le moment est multiplié par cos2(80°) soit 0,03. On ne dispose plus que de 3 % du couple initial. Pour 1 % l’écart avec la direction du vent est d’environ 6 °.
A.V - Moment contraire
Les girouettes sont rarement comme représentée fig 4. En général, on a de la matière de part et d’autre de l’axe, sinon la girouette est déséquilibrée et les frottements augmentent. La matière qui est du mauvais coté présente une surface au vent qui produit un moment en sens opposé à celui qui est utile. Le moment résultant sera la différence entre ces deux moments antagonistes. D’autre part, la matière qui est proche de l’axe n’apporte pratiquement pas de couple mais ajoute du poids donc des frottements. De ce point de vue, la façon dont est réalisé nos coqs de clocher me laisse dubitatif quand à la précision des indications de ces volatils.
A.VI - La force du vent
La force du vent est proportionnelle à la surface et varie avec le carré de sa vitesse.
Pour un vent de 10km/h la force est de 5N/m² (source https://www.toutcalculer.com/sciences/force-vent.php).
A.VII - Moment d’une vraie girouette
Ce moment est complexe à calculer. En effet, tous les points des surfaces de prise au vent ne sont pas à la même distance de l’axe. La valeur exacte fait appel à une intégrale (si la forme peut être mise en équation). Pour faire une évaluation assez correcte, il faudrait diviser la surface en bandes verticales étroites et additionner les moments de chaque bande. Cependant pour un grand rectangle il suffit de considérer la distance D du centre à l’axe. En effet, pour chaque bande située à D – d il existe une bande située à D+d de même surface. On peut donc obtenir une évaluation raisonnable avec quelques gros rectangles, des rectangles moyens et enfin d’autres assez petits.
Donnons tout de suite un ordre de grandeur. Supposons que la surface utile soit de 250cm2 soit 0,025m2 la distance équivalente de 30cm et le vent de 10km/h. On obtient
M = 5 × 0,025 × 30 = 3,75Ncm
A.VIII - Le moment des frottements
Regardons le dispositif de la figure 5. Tous les points de la surface d’appui sont à la même distance R. Le moment de frottement vaut M = P R k où k est le coefficient de frottement que nous estimerons égal à 0,1.
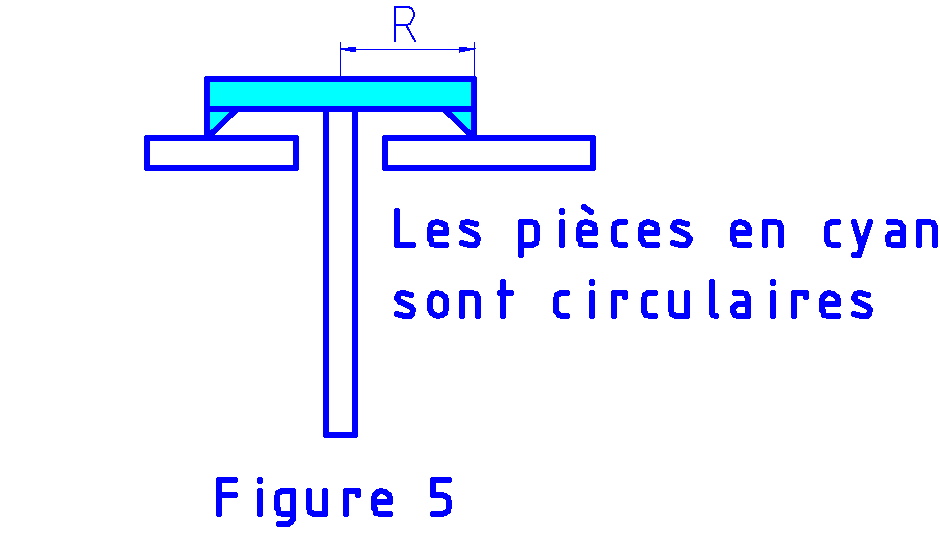
En réalité la surface d’appui n’est généralement pas un cercle mais un disque.
En langage courant, on confond souvent disque et cercle. Pour rester précis : un disque est une surface limitée par un cercle ; le cercle est une ligne, le disque une surface.
Pour un appui en forme de disque, P est soutenu essentiellement par des points plus proches du centre que le cercle limitant et donc le moment résultant est inférieur à ce qu’on vient de calculer. Je vous fait grâce du calcul de l’intégrale. Le rapport est de 2/3.
A.VIII.a - Deux billes l’une sur l’autre
Plus le disque d’appui sera petit, plus le couple de frottement sera réduit. Une bonne solution consiste à placer deux billes d’acier l’une sur l’autre. Mathématiquement la surface d’appui est nulle. Physiquement aucune surface d’appui ne peut être nulle car on aurait alors une pression infinie. En fait, le métal s’écrase très, très légèrement. Le calcul est complexe. Vous trouverez ici :
http://y.callaud.free.fr/hertz.html
un fichier de calcul très bien fait. Les modules d’Young proposés correspondent à de l’acier, n’y touchez pas. Cliquez sur les valeurs des rayons pour les modifier. Modifiez aussi la charge (le poids de la partie mobile – disons 2N soit environ 200g-), le calcul se fait tout seul (fichier Excel).
Pour deux billes d’acier de 8mm de diamètre supportant un poids de 2N (environ 200g) le cercle d’appui fait environ 0,03mm de rayon. Le vrai calcul du moment de frottement est compliqué par le fait que la pression n’est pas uniforme sur tout le cercle de contact. On se contentera ici d’un calcul pessimiste. N’oublions pas que nous ne recherchons que des ordres de grandeurs.
Le moment calculé en supposant la force réparti uniquement sur le cercle serait de 2 × 0,03 × 0,1= 0,006 Nmm.
Le moment intégré sur toute la surface du disque de contact avec une pression uniforme serait de 0,004Nmm.
Le rapport entre le moment moteur calculé ci-dessus et ce moment résistant est de :
3,75 / 0,004 = 937,5 ce qui est excellent. Mais n’oublions pas qu’il s’agit du cas où la girouette est perpendiculaire au vent et qu’à 6° d’écart par rapport à la direction du vent, il ne nous reste que 1 % de la valeur initiale, soit tout de même 9 fois plus que nécessaire. La girouette fonctionnerait encore très bien avec un vent en-dessous de 5 km/h.
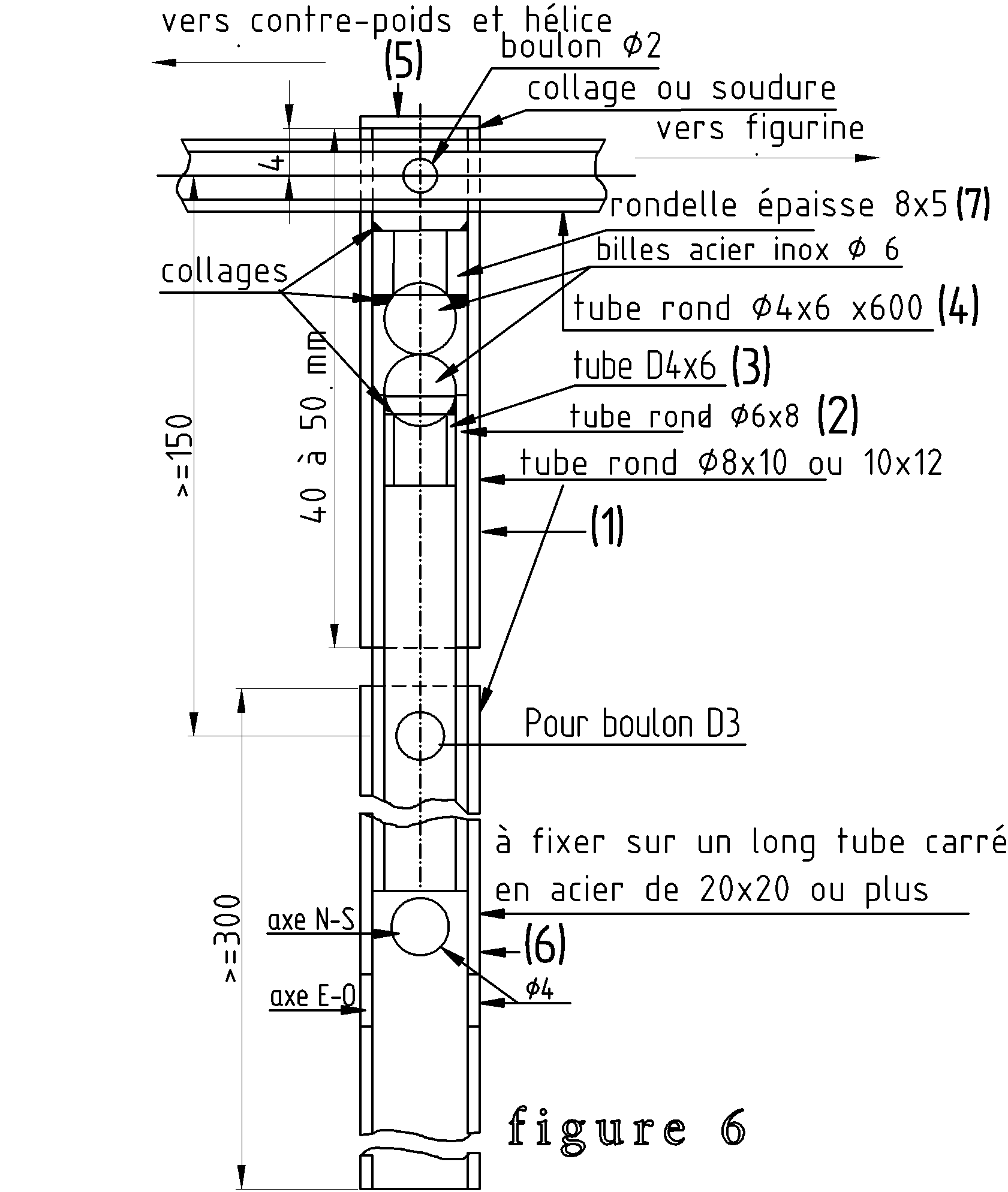
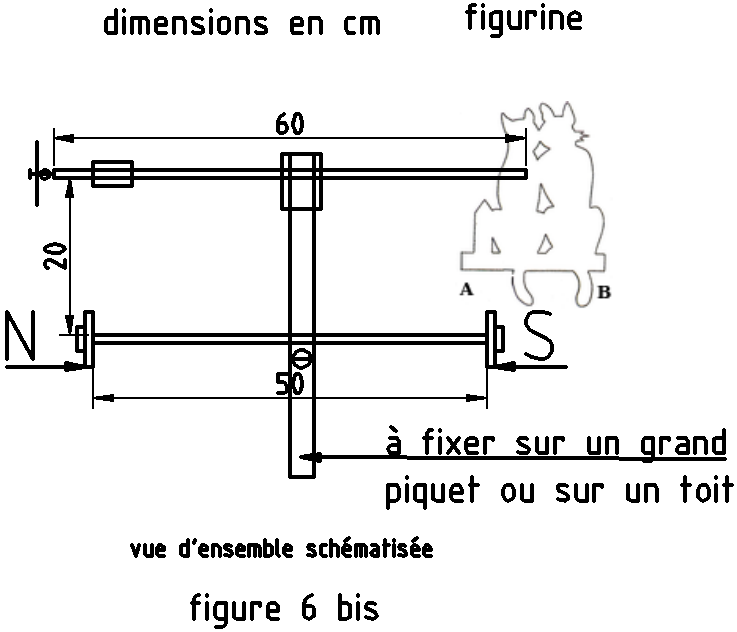
Toutefois ce dispositif est bien théorique. En pratique, il n’est pas stable tel quel. On devra introduire d’autres pièces pour assurer le maintient des 2 billes et donc des frottements supplémentaires. La figure 6 donne un exemple de dispositif qui fonctionne plutôt bien moyennant un bon équilibrage et une parfaite verticalité du support pour réduire les frottements entre les pèces (1) et (6). La figure 6 bis montre une vue simplifiée de la girouette complète.
A.VIII.b - Une bille dans une ‘’cuvette’’ sphérique
Mon idée (originale?) consiste à placer la bille tournante dans une cuvette sphérique. Le système est auto-centreur : si la bille s’écarte du fond de la cuvette, elle tend à y revenir d’elle même. Il n’y a pas d’autres frottements que le contact bille-cuvette.
Vous pouvez reprendre le calculateur ci-dessus. Pour le rayon de la cuvette, il faudra donner un rayon négatif et un module d'Young de 69000 car la cuvette sera en tôle d'aluminium.
La figure 7 montre une coupe du dispositif.
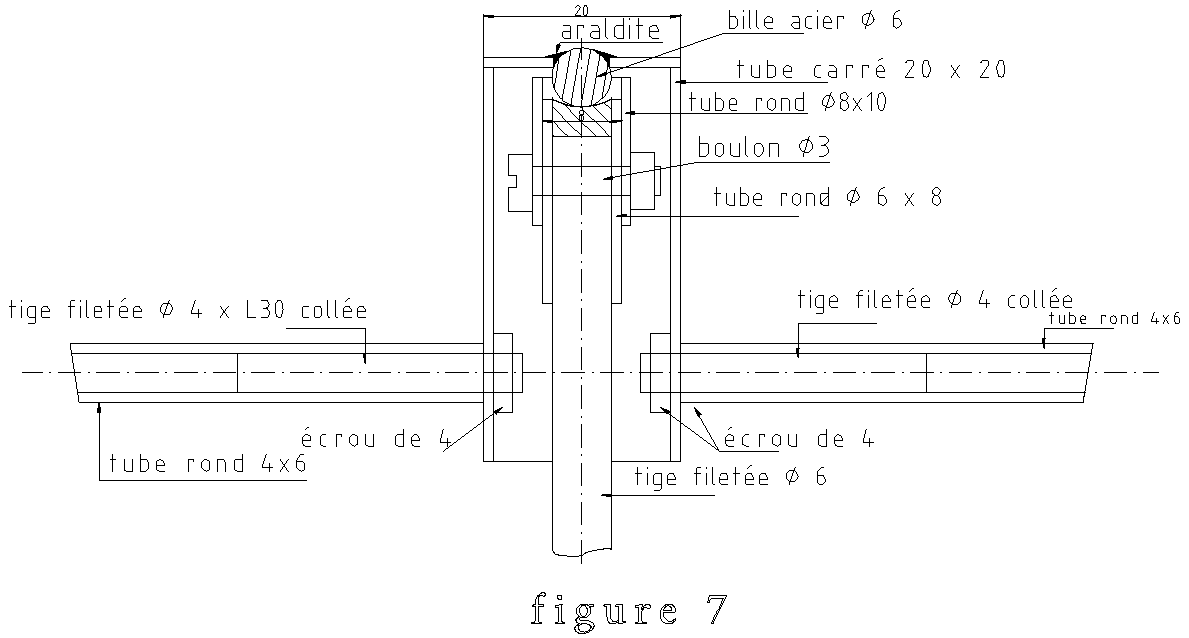
La cuvette telle que présentée sur la figure 7 peut être réalisée facilement. Voir cet article.
A.VIII.c - Le même renversé
On peut concevoir le même couple bille plus cuvette mais retourné. La bille est fixe et la cuvette est placée dessus retournée. L’avantage réside dans la possibilité d’utiliser une cuvette plus large, plus facile à se procurer ou à réaliser.
C’est le système dont je vous propose la réalisation détaillée ci-dessous.
La figure 8 montre une coupe du dispositif en partie haute (ce qui pivote).
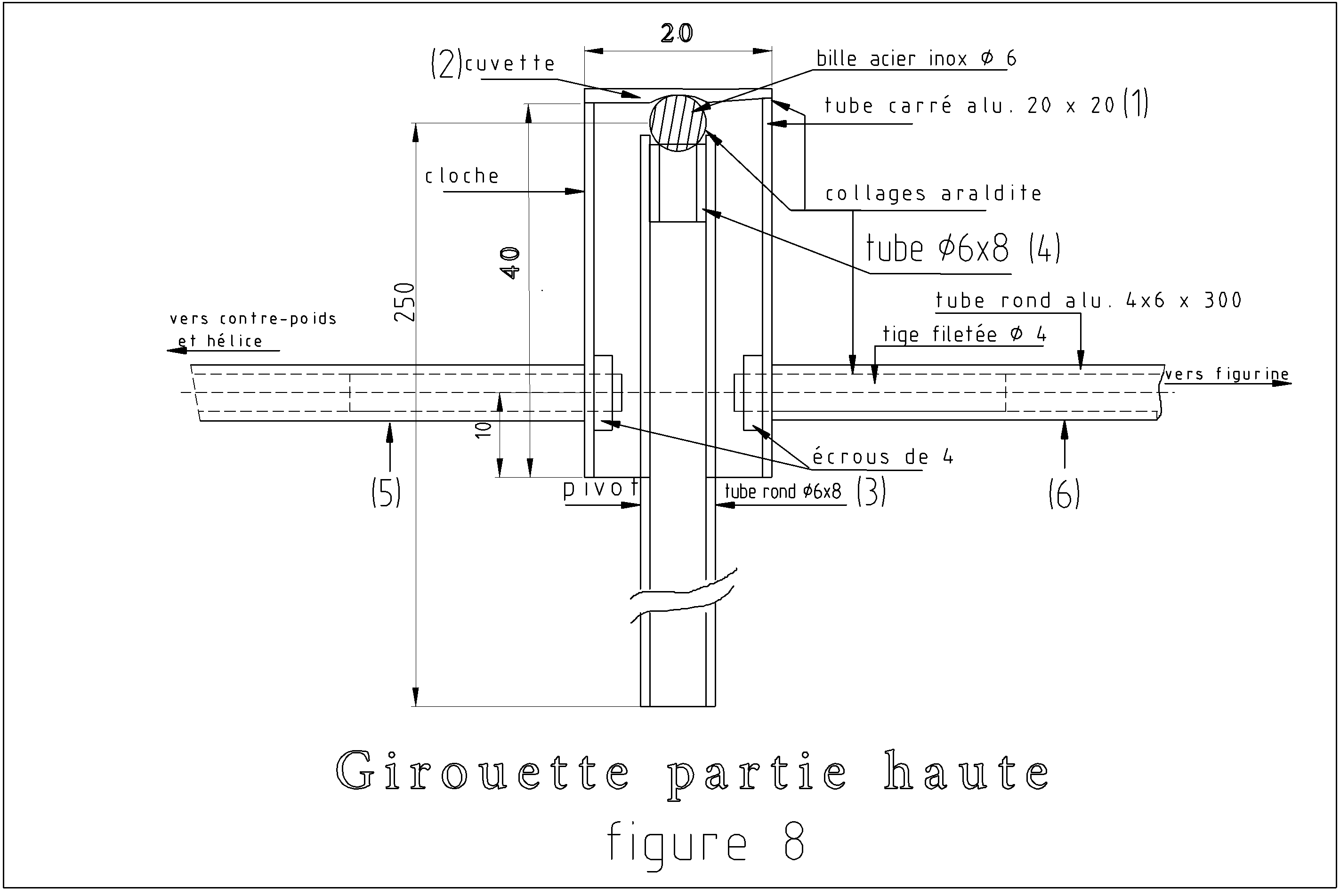
A.IX - Une hélice, pour quoi faire ?
Quand la girouette ne bouge pas, on ne sait pas à priori si c’est parce que le vent est stable et qu’elle s’est arrêtée dans sa direction, ou bien s’il n’y a pas de vent et que la direction de la girouette ne correspond à rien d’actuel. Une petite hélice placée à la pointe de la girouette nous donnera l’information manquante et une vague idée de la vitesse du vent.
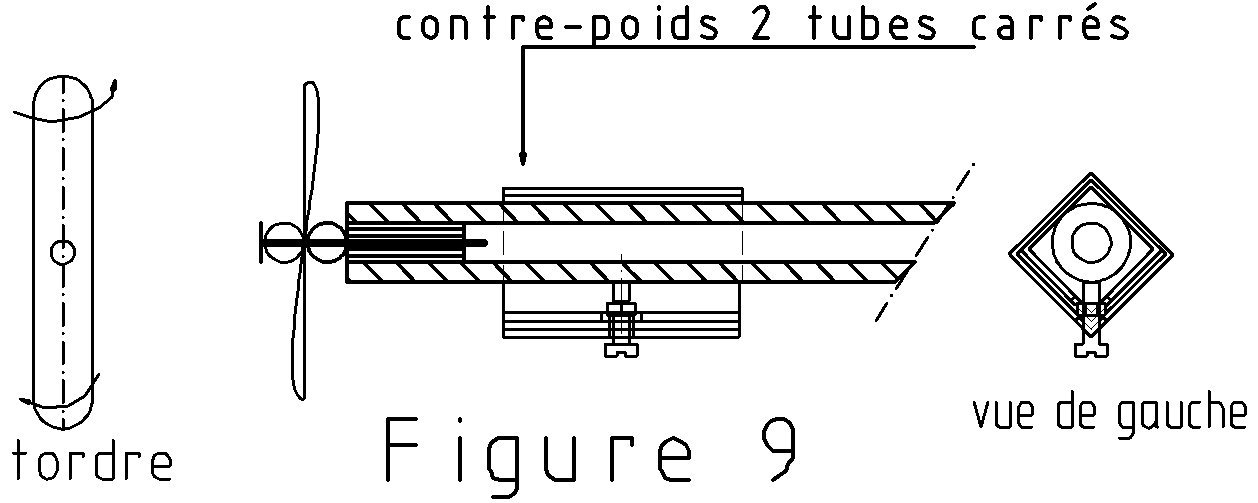
Sur la figure 9, on voit aussi un contre-poids destiné à équilibrer la partie mobile (cloche). Cette pièce est excentrée pour permettre l’équilibrage vertical nécessaire parce que la figurine n’est pas exactement sur l’axe du tube.
B - Réalisation
Rappel préliminaire : Les gens confondent souvent boulon et écrou. En réalité, un boulon est l’association d’une vis et d’un écrou.
Quand je parle de tube D6x4 il s’agit de tube rond de diamètre intérieur 4 et extérieur 6. Quand je parle de tube carré 15x15 ce sont les dimensions extérieures. D8 indique un diamètre de 8mm.
B.I - La ‘’figurine’’
J’ai trouvé ma figurine (ce n’est pas exactement une figurine mais je n’ai pas trouvé d’autre mot) ici : https://pixabay.com/fr/photos/girouette-chat-vent-2678133/.
Il faut s’inscrire pour avoir la version la mieux résolue, indispensable car on n’utilise qu’une petite partie de l’image.
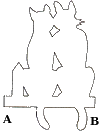 J’ai rogné l’image pour ne garder que les chats. Imprimer les chats noirs tels quels serait un fameux gâchis d’encre et le papier gondolerait à coup sûr. J’ai donc extrait le contour avec Gimp. La figure montre le résultat (en faible résolution par respect pour pixabay). L’image rempli au mieux une page A4. Reporter le contour sur la tôle au feutre fin.
J’ai rogné l’image pour ne garder que les chats. Imprimer les chats noirs tels quels serait un fameux gâchis d’encre et le papier gondolerait à coup sûr. J’ai donc extrait le contour avec Gimp. La figure montre le résultat (en faible résolution par respect pour pixabay). L’image rempli au mieux une page A4. Reporter le contour sur la tôle au feutre fin.
On découpe la figurine dans de la tôle d’aluminium de 0,5mm d’épaisseur à l’aide d’une scie à chantourner. J’en ai une manuelle dont la lame est une sorte de lime ronde. C’est génial, on peut changer de direction sans tourner la scie ! Il existe des modèles torsadés qui doivent faire à peu près la même chose. Certaines parties peuvent être découpées à la scie sauteuse et d’autres à la cisaille. À vous de voir. Ébavurez et finissez à la lime douce.
Si vous souhaitez peindre la figurine, poncez au papier de verre fin, rincez abondamment, appliquez une sous-couche d’accrochage avant la couche de peinture finale.
L’extrémité du tube qui reçoit la figurine est aplati sur 5 cm, au moins (serrez progressivement dans l’étau cm par cm. Finissez au marteau), et percé en 2 points espacés de quelques cm. La figurine est fixée dessus par deux petits boulons de diamètre 2,5mm.
B.II - La construction de la solution à 2 billes
Je vous laisse vous débrouiller avec les figures 6 et 6bis. Le but de cet article étant essentiellement d’exposer ma solution avec une seule bille et une cuvette.
Deux remarques cependant :
1)Pour réduire le plus possible les frottements, le vent ne doit pas créer un couple qui tendrait à faire tourner la figurine suivant un axe horizontale. Ce serait le cas, par exemple si on avait plus de surface en bas qu’en haut. Le bon équilibre se vérifie en posant la figurine à plat sur un objet quelconque présentant une arête vive rectiligne . L’arête doit suivre la future ligne de fixation. On recherche alors le point de basculement limite (voir photo suivante). Pourquoi ça marche ? Parce-que la surface est homogène donc chaque cm² a le même poids et procure un couple proportionnel à sa distance à l’axe. Quand la figurine est verticale, le vent produit le même effet horizontalement que la pesanteur verticalement : chaque cm² procure un couple proportionnel à sa distance à l’axe. L’ensemble de ces couples s’annule.

La figurine est en limite de basculement autour de l’arête AB. Noter que AB doit être parallèle à CD.
2) Le centre de gravité du bras de girouette complet doit être plus bas que le point de contact des 2 billes (équilibre stable). Le contre-poids décentré y contribue mais sera sans doute insuffisant. Il faudra alors charger un peu le bas de la figurine par exemple avec des boulons placés tout en bas.
Lire ce qui est dit sur l’équilibrage du bras de girouette plus bas.
B.III - Construction de la solution avec une bille et une cuvette
Se reporter aux figures 8, 10 et 10 bis et aux photos finales.
matériaux :
Une plaque de tôle d’aluminium format 25 × 50cm environ épaisseur 0,5mm
Une bille acier (inox de préférence) D 6 ou 8.
Vous pourrez trouver des billes de toutes tailles et en faible quantité ici : https://www.123roulement.com/accessoire-bille-BA-8.php*+.
1 tube carré alu 20x20 1m
1 tube D6 × 8 ,,,,,,,,,,,,,,,,,,,,,
2 tubes ronds alu D4x6 1m
1 manchon hexagonal taraudé D8
1 tige filetée D4 1m
4 écrous borgnes D4 et 2 écrous D4 .
1 tube carré en acier (plus peinture) d’au moins 2m le tube carré de 20x20 doit pouvoir entrer à l’intérieur.
colle araldite
Plus quelques babioles qui traînent toujours dans une antre de bricoleur.
Outillage :
réglet
feutre fin
scie à métaux
scie à chantourner
perceuse + perceuse à colonne recommandée
divers forets métal2,5 ; 3 ; 3,5;4 ; 8 (j’en oublie peut-être)
éventuellement quelques forets plats voir figure 11.
tarauds D3
Réalisation :
Commencez par réaliser la cuvette : Découpez dans de la tôle de 0,5mm d’épaisseur, un carré de 30x30mm. Tracez les diagonales. Entre les mors d’un étau, placez l’empilement suivant : une bille d’acier de 12mm de diamètre, le carré de tôle et un bout de planche de bois tendre (sapin) d’au moins 1cm d’épaisseur de quelques cm de coté de plus que la tôle. Ajustez le placement de la bille au croisement des diagonales de la tôle. Repérez l’écartement des mors quand l’ensemble est à peine serré. Serrez l’étau pour réduire l’écartement de 3mm. Desserrez et libérez tout.
Dans un petit bout de planche, percez un trou de D10. Placez la cuvette sur l’établi, bosse en haut puis le trou de la planchette autour de la bosse puis une autre planchette par dessus et pressez fortement le tout pour redresser les bords de la cuvette.
Dans du contre plaqué de 4 ou 5mm découpez un carré de 20 × 20 et percez un trou au diamètre de la bille au point de croisement des diagonales. Placez la bille dans la cuvette, puis le carré de contre plaqué autour de la bille. Tracez sur la tôle le contour du carré ; découpez à la cisaille suivant ce tracé. Ainsi, le centre de la cuvette sera exactement au centre de la cloche.

La « cloche » pièce (1) figure 8 et 10bis se réalise en débitant 40mm dans du tube carré de 20 x20 ou 18x18(un peu juste à cause des écrous de fixation des bras de figurine et de contre-poids).
Percez les deux trous du bas en vis à vis à 10mm de l’extrémité D = 4
Débitez 2 pièces de 300mm et 4 de 235mm dans du tube d’aluminium de D4x6.
Débitez dans de la tiges filetée D4 2 bouts de 500 mm et 2 bouts de 40mm de long (ou coupez la tête de 2 vis).
Coupez un petit bout de tube (10 à 20 mm) D6x4 (pièce (4). Enfilez le dans le tube (3) un peu en retrait de l’extrémité. Fixez avec un boulon de D2,5 ou 3.
Collez la cuvette à l’araldite. Collez la bille sur le tube 6x6. Chargez en araldite les 2 bouts de tige filetées de 40mm en laissant 1cm sans colle et introduisez les dans les tubes de 300mm (11) et (12) en ne laissant dépasser que 3 ou 4mm. Essuyez la colle qui déborde du tube.
Laissez prendre la colle en lieu sûr pendant 24h.
Pendant ce temps, dans le tube carré de 15x15 percez les 2 paires de trous pour les 4 bras azimutaux. (figure 10 bis).
Coupez en 2 parties sensiblement égales un manchon taraudé de D8. Chaque pièce (8) et (9) sera appelée manchon par la suite.
Percer à D8 le trou taraudé des 2 manchons en utilisant un étau à main et une perceuse à colonne de préférence.
Pointez le perçage à 2,5 du milieu d’une face de chaque manchon.
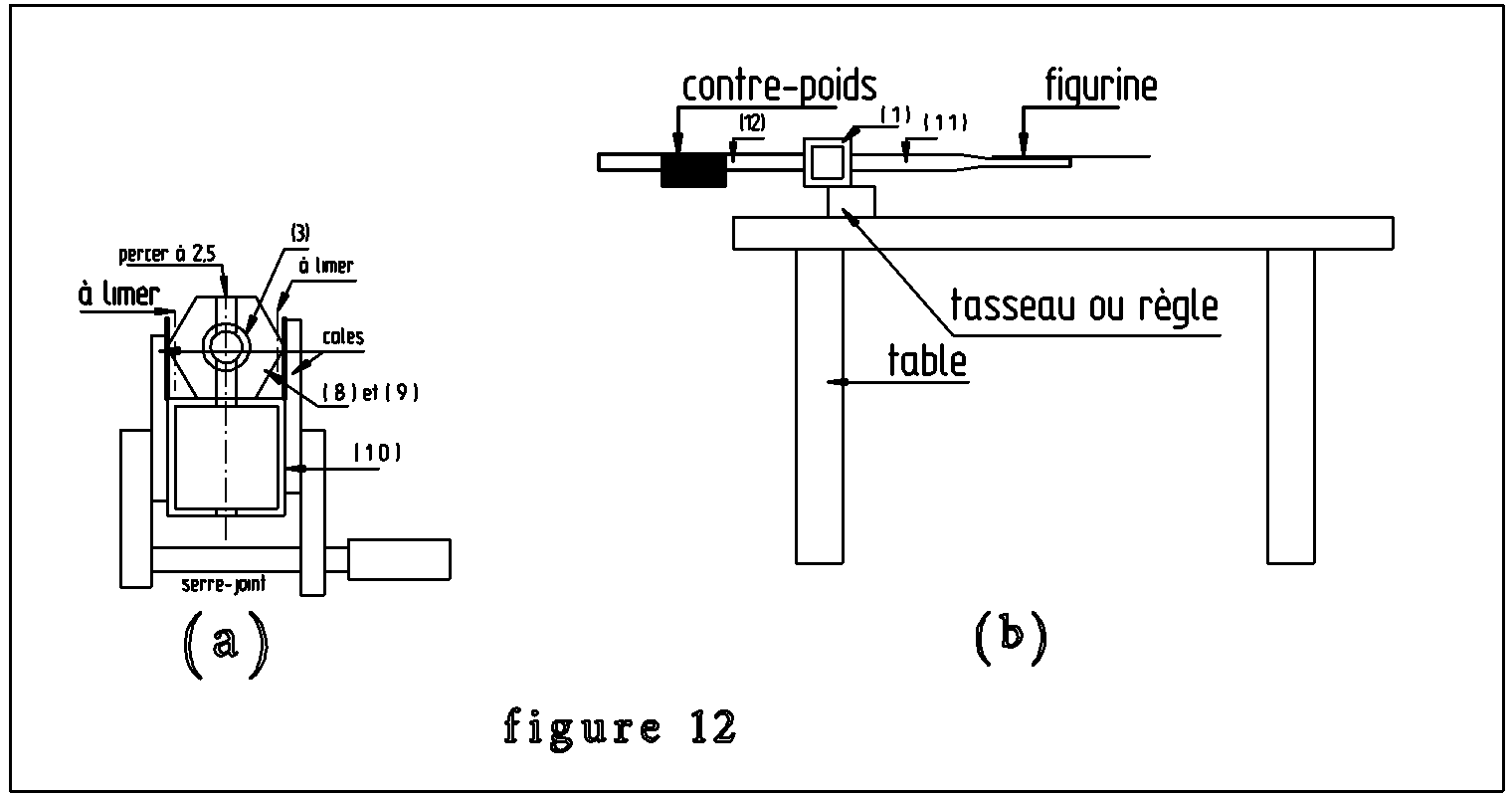
Enfilez les manchons sur le tube (3) comme indiqué figure 10bis. Posez l’ensemble sur le tube (10) Pour centrez sur la largeur et faire tenir en place, serrez ensemble deux cales sur les faces verticales avec un serre-joint et coincez les manchons avec des petites chutes de tôle (figure 12(a)). Percer à la perceuse à colonne, à D2,5 les manchons et les tubes (3) et (10) pour que les distances soient parfaitement égales. Désassemblez et repercez les pièces (3) et (10) à D3,5.
Taraudez à 3 les 2 manchons de part en part. Attention, ces petits tarauds sont fragiles. Ne forcez pas, revenez souvent en arrière pour casser le copeau.
La clé des manchons fait 13 mm comme l’intérieur du tube de 15x15, mais entre deux arêtes opposées il y a plus. Il faut donc limer fortement et symétriquement les 2 arêtes qui n’appartiennent à aucune des faces taraudées (figure 12(a)), pour que le manchon puisse entrer dans le tube de 15x15.
NB : Si vous utilisez du tube de 20x20, vous n’aurez pas à limer les manchons mais vous devrez placer des entretoises pour centrer (3) dans (10).
Présentez les manchons dans le tube carré (10) à l’emplacement prévu (figure 10 bis) et vissez une vis de 3 x15 sur chacun.
Le manchon du fond risque d’avoir du mal à s’enfoncer tout en restant au bon niveau par rapport à (3). Une solution consiste à introduire un petit clou de D2 de longueur 10mm environ dans le manchon et dans le tube (3). Une fois en face du trou de (10), la vis le repoussera en se vissant.
Écrasez le tube (11) sur environ 5cm en le serrant progressivement dans un étau puis en le martelant de façon à faire un plat pour la fixation de la figurine.
Pour le placement de la figurine par rapport au tube (11), voir en B-II. 1). Le point 2) ne nous concerne pas.
Reprenez la cloche. Fixez le tube (11) avec la figurine, sur la cloche avec un écrou de D4.
Fixez le tube (12) de l’autre coté.
Ce tube porte un contre-poids destiné à équilibrer la girouette. La rotation du contre-poids le déporte légèrement à droite ou à gauche, (vu en bout, voir figure 9) de façon à assurer l’équilibrage vertical pour compenser le petit décalage par rapport à l’axe de la figurine.
Le contre-poids est réalisé avec deux bouts de tubes carrés entrant l’un dans l’autre. Au milieu d’une arrête, on lime pour faire un plat puis on perce à D 4,5mm pour le plus gros tube et à 8 pour le petit. Il faut alors introduire un écrou par l’intérieur du petit tube et visser une vis D4 depuis l’extérieur. Voir la photo à la fin.
L’opération n’est pas très aisée. Serrez les tubes dans l’étau entre deux arêtes (oui ça a tendance à riper. Utilisez si possible 2 Vés de guidage), l’arête percée placée en haut. Vous pouvez utiliser une petite bande de métal de quelques mm de large. L’écrou est collé à une extrémité avec de la pâte à fixer. Pour visser, il faut tirer sur la vis pour plaquer l’écrou contre le tube afin de l’empêcher de tourner.
Pour déterminer la longueur définitive du contre poids : posez le, la cloche couchée sur une règle ou un tasseau posée sur une table au niveau du petit trou (figure 12(b) et photo) ; placez le contrepoids sur le tube (12) et rapprochez le plus ou moins de la cloche jusqu’à obtenir l’équilibre (ou presque). Mesurez d1 la distance entre le milieu du contre-poids et l’axe de pivotement. Déduisez de la position du contre poids la longueur finale sachant qu’il vaut mieux qu’il soit fixé près de l’extrémité du tube.
Calcul de la longueur finale Lf: Il y a équilibre lorsque le produit L × d = une constante K, où L est la longueur du contre-poids et d la distance. Le premier essai nous donne l’équilibre à une distance d1 (comptée du milieu du contrepoids au trou central du tube ( 4) pour L1= 10. On a donc K = 10 × d1. Pour une distance recherchée df on a aura une longueur finale Lf = K / df.
À l’extrémité de ce tube, on enfile une cheville en nylon D4. Dans cette cheville, on met une vis sur laquelle on a, au préalable, enfilé une perle de verre une hélice découpée dans la même tôle que la figurine et une autre perle (figure 9).
Découpez dans la même tôle que la figurine les lettres N, S, E et O et percez un trou D4 dans chacune pour la fixation.
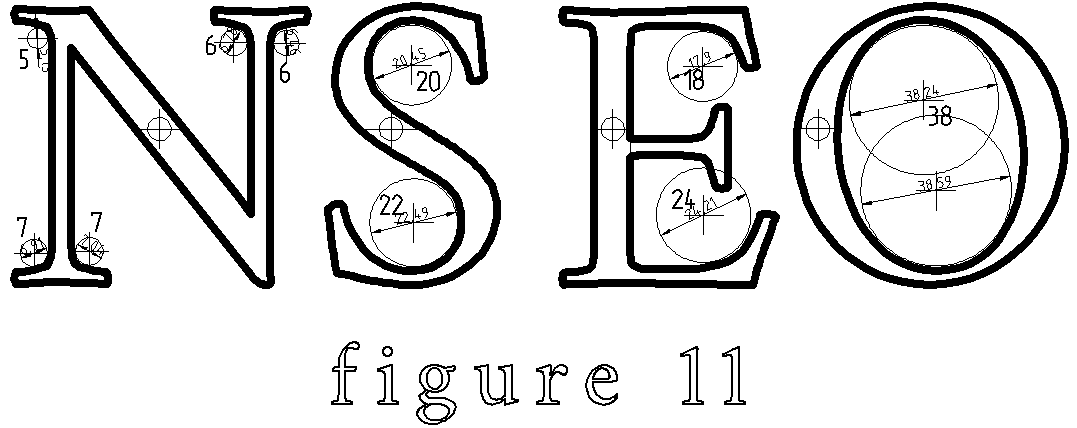
La figure 11 propose un modèle de lettres (issu de Librecad). La taille doit être de l’ordre de 6cm de haut.
Certaines parties peuvent être approximées par des arcs de cercles et donc découpées au foret. Utilisez des forets plats pour les diamètres à partir de 18. Pour le ‘’O’’ on ne pourra percer qu’un seul cercle de D38. Les diamètres affichés sont à vérifier en fonction de la taille d’impression.
Prendre un rectangle de tôle alu 0,5mm pouvant contenir toutes les lettres. Coller du scotch double face pour couvrir toute la surface du rectangle. Coller la feuille de lettres. Percez tous les trous (les trous de fixation, non cotés sont à percer à D4.); découpez à la cisaille et à la scie à chantourner. Ébavurez et finissez à la lime douce.
Pour les lettres N et S : passer une lettre sur l’extrémité d’une des 2 tiges filetées de 500mm; vissez un écrou borgne à fond sur la même extrémité; enfilez un tube D4x6 de 250mm jusqu’au contact avec la lettre ; enfiler la tige filetée sur le tube carré (10) ; enfilez un 2e tube de 4x6, puis l’autre lettre, un écrou et serrez. Ajoutez un écrou borgne pour l’esthétique.
Recommencez avec les lettres E et O dans une direction perpendiculaire, un peu en contre bas. Vérifiez la cohérence des indications.
Posez la cloche sur la bille et vérifiez que ça tourne bien (un léger souffle devrait suffire.) et que la girouette ne vient pas buter dans les lettres. Si c’est le cas, réduire la longueur des bras azimutaux.
Enfilez le support vertical (10) dans un grand tube d’acier (au moins 2m de long) à ficher en terre aussi verticalement que possible (mais vous avez droit à une marge d’erreur).
N’oubliez pas d’orienter convenablement les bras azimutaux. Pour trouver le nord, utilisez une boussole, repérez l’étoile polaire ou utilisez un logiciel tel que Stellarium ou un éphéméride pour savoir quand le soleil est exactement au sud ; guidez-vous sur l’ombre.
Le tube carré d’acier de 2m de long ou plus sera préalablement peint coté intérieur autant qu’extérieur avec une peinture extérieure anti rouille. Pour peindre l’intérieur, faire couler la peinture dans un sens puis dans l’autre en tournant d’un quart de tour à chaque fois. Faire sécher verticalement en récupérant le surplus dans une boite de conserve. Faire reposer le tube sur une grosse vis pour que le surplus se détache du tube.
En complément, deux photos pour ceux qui n’aiment pas les dessins techniques.
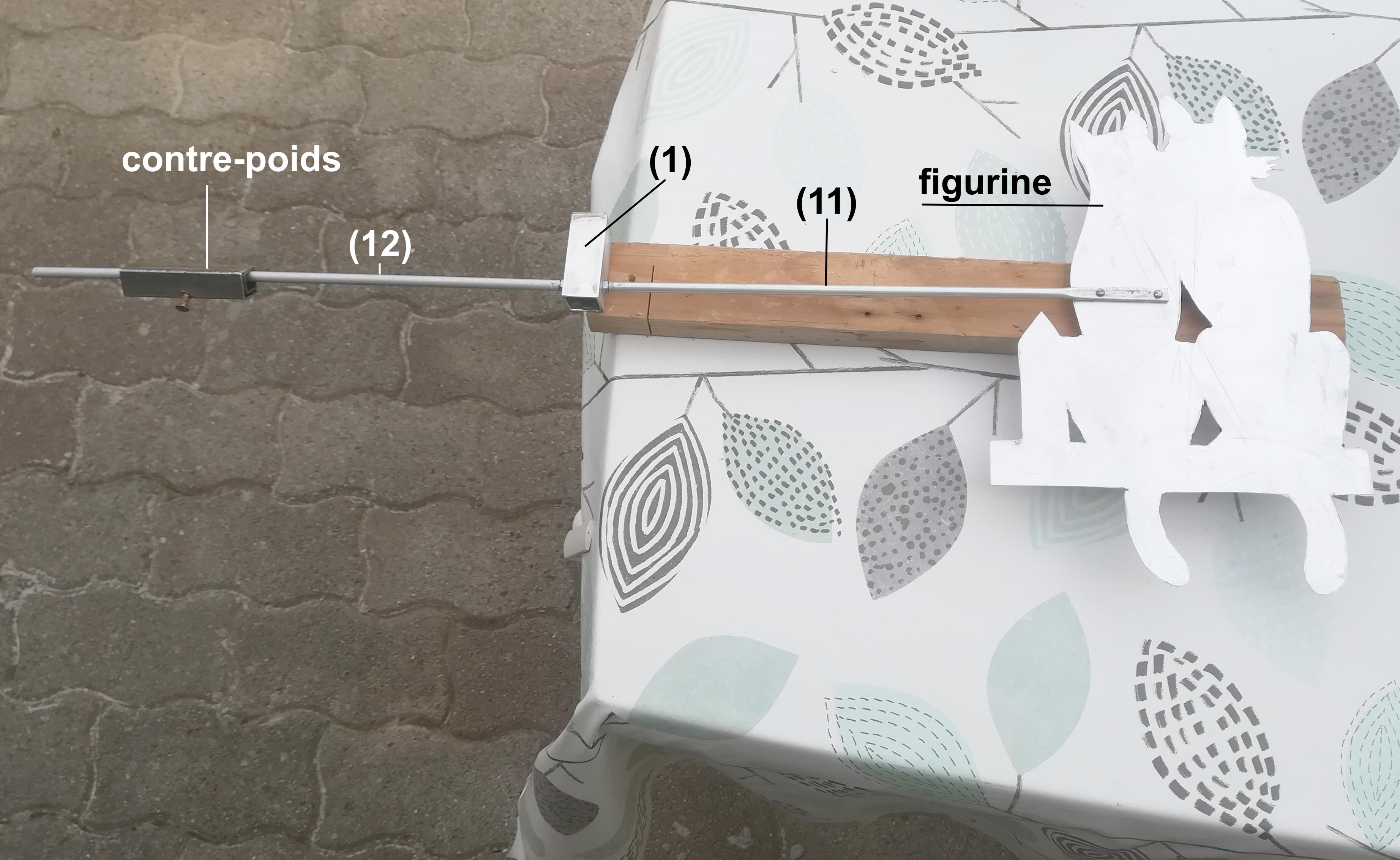
La procédure d’équilibrage

Le pivot et les bras azimutaux. La cloche a été retirée.
Bon vent !
***** © M Guignard *****


Comments powered by CComment