Centres et diamètres

Les pièces circulaires posent deux sortes de problèmes. La mesure de leur diamètre et le repérage du centre. Ce texte propose diverses solutions pour résoudre ces problèmes.

Le pied à coulisse apparaît souvent comme l'outil idéal qui mérite largement son investissement. Cependant on n'en a pas toujours un sous la main et au delà d'un certaine diamètre il devient inutilisable. C'est pourquoi certaines astuces présentées ici peuvent souvent être utiles.

A -Mesure du diamètre

La mesure du diamètre ne présente pas les mêmes difficultés pour les pièces mâles (en relief) et les pièces femelles (en creux).

A.I -Les pièces en relief

Le pied à coulisse est l'outil idéal, dans sa gamme de dimensions. Son utilisation ne pose pas de problème particulier ici à condition de savoir lire ses graduations mais ceci est une autre affaire.

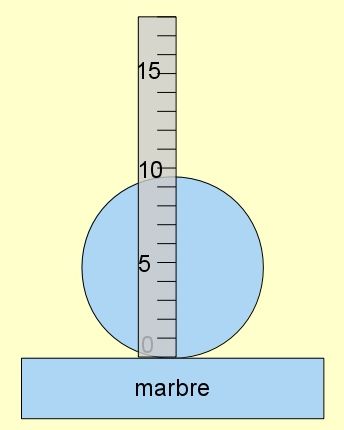
Le réglet se prête plus ou moins bien à la mesure des diamètres. Je recommande de procéder de la façon suivante : poser l'objet à mesurer sur une surface plane (marbre) de telle sorte que la surface circulaire soit perpendiculaire au plan du marbre. Plaquer le réglet sur la surface circulaire, les graduation sur cette face, le zéro sur le marbre. Lire la graduation tangente sur le dessus de la face circulaire.

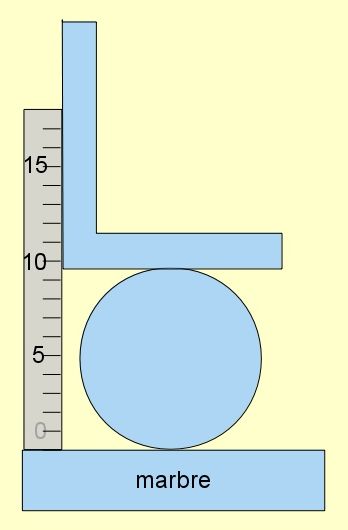
Vous pouvez aussi, décaler le réglet et appuyer une équerre le long du réglet et sur la pièce à mesurer.

Voici maintenant quelques astuces assez connues mais bien utiles parfois.

• Utiliser une clé à fourche : chercher la clé qui rentre pratiquement sans jeu.

• Serrer l'objet dans une clé à molette puis mesurer la distance entre les deux mâchoires.

• Pour les petits diamètres, introduire la pièce dans un trou d'une boîte à forêts.

• Pour les tout petits diamètres de fils: Enrouler le fil à spires parfaitement jointives sur un support cylindrique et diviser la longueur du bobinage par le nombre de spires.

   

• Coincer la pièce entre 2 règles. Mesurer la distance entre les règles aux deux extrémités. Corriger la direction jusqu'à ce que les distances soient égales. À ce moment, les règles sont parallèles et la distance est égale au diamètre. Les choses sont plus simples si on dispose de deux exemplaires identiques de l'objet à mesurer, ou de 2 équerres.

• Dans certains cas, il est plus simple de mesurer la circonférence, avec un mètre de couturière par exemple ou avec une ficelle en reportant la longueur repérée sur un mètre à ruban ou un réglet. Le diamètre se détermine avec un petit calcul:

D= C / π

où D est le diamètre, C la circonférence (même unité pour les 2) et π = 3,14 pour un usage courant ou 3,1416 pour les pinailleurs.

A.II -Les pièces en creux, les diamètres intérieurs

Le pied à coulisse reste un bon outil, avec un petit bémol cependant. On n'est jamais tout à fait sûr de mesurer un vrai diamètre et non une corde très proche mais pas exactement un diamètre. Seule solution insister et retenir la mesure la plus élevée : on peut être en dessous mais jamais au-dessus du diamètre.

Le réglet fait ici ce qu'il peut. Ne pas espérer trop de précision.

Pour les petits diamètres, introduire la queue d'un foret.

A.II.a -Les cas difficiles

Je pense ici au formes complexes comme un bocal à poisson rouge ou une bouteille. On peut utiliser ou se bidouiller un compas maitre de danse (quel joli nom !). Les pointes de pieds du « danseur » viennent en

contact avec les parois internes ; on mesure l'écart entre les extrémités des bras ; on ressort l'instrument ; on recrée le même écart des bras et ou mesure l'écart des pieds. Attention cependant, on fait trois mesures, la somme des erreurs peut être conséquente.

Le cas de la bouteille est encore plus difficile, à cause de l'étroitesse du goulot. Je propose une méthode détournée. On verse un peu d'eau dans la bouteille de façon à échapper à la forme courbe du fond. On mesure la hauteur h0 du liquide par rapport à la table où est posée la bouteille. On verse ensuite une quantité d'eau connue, par exemple un demi litre. Il faut monter assez haut pour avoir le plus de précision possible mais sans atteindre la zone où le diamètre se réduit. On mesure à nouveau la hauteur h1. Il n'y a plus qu'à faire un peu de calcul pour déduire le diamètre D du volume V.

Calculer H = h1 – h0 (en cm)

Exprimer V en cm3 ex 0,6litre = 600 cm3 ou 600ml

Calculer D² = 4 × V / H / π

Calculer la racine du résultat précédent

Ex h0 = 2,4cm ; h1 = 15,6cm ; V= 0,7litre

Faire 15,6 – 2,4 = on obtient H = 13,2cm

ensuite 4 × 700 donne 2800 divisé par 13,2 donne 212,121... divisé par π donne 67,52 et la racine carrée de ce nombre est 8,217. Notre diamètre est donc de 8,2cm ou 82mm.

Et si la bouteille est opaque? Dans ce cas, vous pouvez piquez une aiguille à tricoter dans un bouchon qui passe facilement par le goulot; vous mettez le bouchon dans la bouteille (il faut qu'il flotte). Vous faites un repère sur l'aiguille à l'endoit où elle sort du goulot avant et après remplissage. H est la distance entre vos deux repères.

B -Marquage du centre

B.I -Les pièces en relief

Le meilleur outil pour repérer le centre est sans doute le trusquin de mécanicien. Cet outil est assez méconnu. Il permet pourtant des tracés extrêmement précis. Voir l'article de Wikipédia à http://fr.wikipedia.org/wiki/Trusquin.

On place l'objet sur un marbre, la face circulaire perpendiculaire au plan du marbre. Pour une pièce de faible épaisseur, style pièce de monnaie, on s'appuiera sur une équerre de mécanicien. Dans un premier temps, le trusquin peut servir à déterminer le diamètre de la pièce. Celui-ci étant connu, on règle le trusquin à la moitié de ce diamètre. On trace alors un petit trait à l'endroit présumé du centre sans que la pièce bouge. On recommence 3 fois en faisant tourner la pièce de 90° à chaque fois. Si tout est parfait, les 2 premiers traits suffisent, les autres retombent dessus. Sinon on obtient un petit carré : le centre est au point de rencontre des diagonales.

Si on n'a pas de trusquin, on peut découper dans du carton mince, une bande assez longue et de largeur égale au rayon. On pose une longueur sur le marbre et l'autre longueur sert de guide pour tracer les 4 petits traits comme ci-dessus. Cette fois ci, on aura certainement un petit carré. Tracer les diagonales très soigneusement.

B.II -Les pièces en creux, les diamètres intérieurs

Cette fois ci, le centre est immatériel ! Et pourtant on peut en avoir besoin. Ex. : On dispose d'une rondelle et on veut tracer un cercle concentrique de diamètre intermédiaire entre le diamètre intérieur et le diamètre extérieur. Une bonne solution est de s'aider d'un carré de cotés égaux au diamètre extérieur. Le point de concours des diagonales marquera le centre des cercles dès que la rondelle sera placée sans déborder à l'intérieur du carré .

On peut aussi découper un carré ajusté au diamètre intérieur. Là aussi on utilise les diagonales. Pour trouver le coté du carré, il faut diviser le diamètre par racine de 2 soit 1,414.

Autre cas de figure: On veut faire passer un faisceau laser exactement suivant l'axe d'un tube.

Dans une plaque de quelques mm d'épaisseur, on fait une marque au pointeau comme pour percer un trou. On trace un cercle au compas de menuisier en utilisant le pointage comme centre. Le rayon du cercle doit être égal à celui du tube. On trace un autre cercle de même centre mais de rayon 2 mm au-dessus du précédent. On ouvre le compas à 1,732 fois le rayon du 2e cercle. On pique une pointe du compas sur le plus grand cercle et on marque les 2 intersections du compas avec le 2e cercle. On a ainsi 3 points qui déterminent un triangle équilatéral. Remarquer qu'il est sans importance que le triangle ne soit pas tout à fait équilatéral. On découpe le triangle. Si on dévie un peu, ce n'est pas grâve. On émousse les pointes du triangle jusqu'au cercle intérieur, à la lime, en contrôlant souvent, au pied à coulisse, la distance du centre au sommet émoussé. On arrête quand les 3 distances sont strictement égales au rayon du tube. La pièce doit rentrer juste dans le tube qu'elle touche en 3 points. Il ne reste plus qu'à percer un trou au centre des cercles. 

. Deux pièces identiques déterminerons l'axe du tube.

***** ©  M Guignard *****