Draw : à propos des courbes de Bézier

Le tracé des courbes de Bézier n’est pas très facile à maîtriser. Je donne ici quelques points de repères qui éviterons à certains des errements pénibles et chronophages.

Commençons par un exercice tout simple : le tracé d’une pseudo sinusoïde.

A -La pseudo sinusoïde

En électricité et en électronique (entre autres) on a souvent besoin de tracer quelque choses qui puisse passer pour une sinusoïde. Essayez pendant quelques minutes de tracer une courbe de Bézier qui ressemble à peu près à une sinusoïde. Pas facile ! N’insistez pas, lisez la suite.

Commencez par tracer un rectangle : Activez l’accrochage aux points de la grille ; définissez un pas de grille de 1cm ; faites un rectangle de 6cm de large et 15cm de haut.

Soit ABCD ce rectangle. A est en bas à gauche, B en haut à gauche. Soit M le milieu de BC.

B--M---C

A------- D

Prenez l’outil courbe de Bézier (à coté du crayon). Clic-gl de A à M > placez la souris en D > 2-clic. Vous obtenez une courbe qui ressemble fortement à une arche de sinusoïde. Faites un copier/coller (vous ne voyez rien, l’exemplaire collé est superposé à l’original) puis M Modifier > retourner > verticalement. Vous obtenez une arche négative. Déplacez la pour la mettre dans le prolongement de la première arche ( outil de sélection > placer le curseur de souris pour qu’il devienne une croix fléchée, clic-gl) > sélectionnez l’ensemble en l’incluant dans un rectangle débordant très haut de part et d’autre > M Modifier > grouper.

La taille actuelle ne vous convient pas ? Clic en bas dans la barre d’état là où vous lisez la taille et la position de l’objet en cours. Onglet position et taille > dans la rubrique taille décochez au besoin conserver le ratio > changez à votre convenance la largeur et la hauteur. À droite, le point de base est celui qui ne bougera pas malgré les modifications de taille. > OK.

Vous avez une période de sinusoïde ; vous pouvez en placer autant que nécessaire bout à bout avec des copier/coller puis grouper l’ensemble.

B -Comment tracer une courbe quelconque

Expérimentez : Démarrez un nouveau dessin. Faites un rectangle ABCD comme ci-dessus avec le point A dans le bas gauche de la feuille, disons 6cm de large et 10 cm de haut. Dupliquez le et changez la taille à 12cm et 20cm en prenant pour point de base le point bas gauche. Les points du grand rectangle s’appellent AB’C’D’.

Faites une courbe en commençant par un clic-gl de A à C puis en descendant à droite de C avant de faire le 2clic final.

Faites la même chose en allant de A à C’. La courbe obtenue a la même pente à l’origine (en A) mais elle est apte à monter beaucoup plus haut.

Essayez maintenant de faire une courbe en plusieurs sections :

Vous démarrez par un premier clic-gl qui indique la pente à l’origine puis, après relâchement du bouton de la souris, vous vous rendez au deuxième point et vous faites un nouveau clic-gl en arrière (en remontant la courbe). Vous voyez alors un segment bleu pointillé qui vous indique la direction de la tangente. Attention, plus ce segment sera long, plus vous déformerez la partie précédente de la courbe. Lâchez le clic et déplacez la souris vers la suite de la courbe : le « fil de fer » se déplie. Rendez vous au troisième point. Recommencez.

C -Avec des segments de droites

Vous avez pu voir ci-dessus qu’il n’était pas simple de faire passer une courbe de Bézier où l’on veut. Vous pouvez procéder d’une autre manière.

Vous commencez par définir la trame de votre courbe par des segments de droites avec le 2^e outil après le crayon. Puis vous faites M Modifier > convertir > en courbe. Ensuite il faut choisir l’outil de modification des points le premier de cette série   

Les points sont repérés par des petits carrés bleus. Faites au besoin M affichage > barre d’outils > éditer les points. Dans cette nouvelle barre qui s’active quand on clique sur un des points, on a (entre autres) ces trois outils qui définissent le type de points. Le premier définit un point d’inflexion (ou de rebroussement) : la tangente n’est pas la même de part et d’autre du point. Le deuxième définit un point avec deux tangentes alignées : les pentes sont égales de part et d’autre mais n’évoluent pas de la même façon (la courbe se tord plus vite d’un coté). Le troisième outil donne des points symétriques : les pentes sont égales et évoluent de façon régulière autour du point. C’est avec ce troisième outil que nous allons modifier notre courbe en l’appliquant à chaque point.

Ceci : 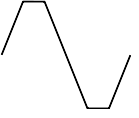vous donne cela :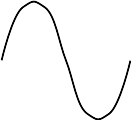

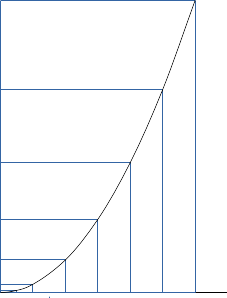une parabole : La grille a été définie avec 20mm en x et 5mm en y sauf pour le plus petit rectangle : 10mm en x et 1,25mm en y. Il suffit de compter. Pour n unités en x on a n² unités en y. Régler à 0 la pente au point de départ.

D -Comment tracer une sinusoïde quasi parfaite

Voici les valeurs des sinus multipliées par 200

Tracez un grand rectangle ABCD (comme en A) de largeur 180mm et de hauteur 200mm.

Faites une série de rectangles ayant tous le point A comme coin gauche du bas et de dimensions données par le tableau. Exemple pour le premier, 10mm de large et 34,7mm de haut. Vous faites d’abord un rectangle de 10mm de large (soit un pas de grille) et de hauteur de 30 ou 40mm ; puis vous cliquez dans la barre d’état. Dans la rubrique taille vous entrez les bonnes dimensions avec conserver le ratio décoché et comme point de base celui du bas gauche > OK.

Faites ainsi pour les 9 rectangles.

Sélectionnez les 9 rectangles puis faites copier coller et M Modifier > retourner >horizontalement. Déplacez l’ensemble pour placer le coin inférieur droit en D.

Faites une ligne brisée partant de A et passant par les points diagonalement opposés des 9 premiers rectangles puis par les points symétriques pour finir en D.

Arrondissez la courbe comme expliqué en C.

Sélectionnez la courbe > redimensionnez la > faites un doublon > retournez le verticalement et collez le au bout de l’original comme décrit en A. Vous avez une période de sinusoïde assez précise.

E -Conclusion

Vous voila un peu moins démunis face aux courbes de Bézier. Vous avez sans doute compris que plutôt que de partir de zéro, il vaut mieux démarrer sur une forme de base. Vous trouverez sur le web des astuces pour tracer diverses formes en partant d’un cercle converti en courbe par exemple (œuf, cœur…).

© M Guignard