Contrôler un équerrage
Les équerres
Pour contrôler un équerrage (un angle droit), on utilise en général une équerre.
Il existe plusieurs sortes d’équerres :
-
L’équerre de dessinateur, simple pièce de plastique plate.
-
l’équerre de menuisier, présente des rebords sur lesquels on peut appuyer l’un des bords à contrôler.
-
l’équerre de mécanicien, plate ou à chapeau.
-
l’équerre de maçon
-
l’équerre de fortune : plier en deux une feuille de papier, soigneusement bord sur bord. Le pli est rigoureusement perpendiculaire aux bords superposés.
- Choisissez celle qui convient le mieux pour le travail à effectuer. Ce ne sera pas toujours celle qui semble naturelle à priori. Pour de grandes pièces de menuiserie, par exemple, une équerre de maçon, plus grande, peut être préférable.
- N’oubliez pas que vous pouvez utiliser l’angle rentrant ou l’angle sortant (sauf pour l’équerre de dessinateur).
Le théorème de Pythagore
Pour les grandes dimensions, l’équerre ne donne pas des résultats assez précis. Il faut avoir recours au théorème de Pythagore.
Je me garderai bien ici d’énoncer ce théorème pour n’effrayer personne. Les curieux pourront regarder ici. En pratique, il suffit de connaître une règle très simple, la règle dite 3, 4, 5 qui en est un cas particulier:
Si on construit un triangle dont les 3 cotés ont pour dimensions 3, 4 et 5 unités, ce triangle est rectangle, c’est à dire que l’angle des cotés de longueur 3 et 4 est un angle droit. L’unité peut être ce que l’on veut : le mètre le décimètre, ou 45 cm si ça vous chante. La seule règle à respecter est d’avoir un coté faisant 3 fois une certaine longueur, un deuxième coté faisant 4 fois cette même longueur et le dernier (l'hypoténuse) 5 fois.
En pratique, on mesure la longueur 3u sur un des cotés de l’angle droit, la longueur 4u sur l’autre coté et on fait tourner un coté pour avoir une longueur de 5 unités exactement entre les extrémités de ces deux cotés (hypoténuse du triangle rectangle).
On peut utiliser d’autre triplets. En voici une liste (tirée de l’article de Wikipédia).
3;4;5 20,21,29 11,60,61 13,84,85
5,12,13 12,35,37 16,63,65 36,77,85
8,15,17 9,40,41 33,56 65 39,80,89
7,24,25 28,45,53 48,55,73 65,72,97
Seuls ceux que j’ai mis en gras me semblent intéressants parce-qu’ils sont équilibrés. J’entends par là que les longueurs des cotés de l’angle droit sont proches l’une de l’autre ce qui est favorable à la précision..
Quand on exécute quelque-chose, il est toujours bon, voir indispensable, d’évaluer les erreurs de réalisation. Posons un problème concret :
On veut réaliser un terrassement rectangulaire de 12m par 15m. On utilise 3, 4, 5 en prenant 1m comme unité. Un coté de 15m sert de base de départ. On doit donc définir deux droites perpendiculaires à cette base, de 12m de longueur. Si on a une incertitude i de 1cm sur la longueur de l’hypoténuse, quelle sera l’incertitude sur la longueur de 15m à l’autre extrémité ?
La figure ci-dessous montre ce qu'il se passe dans le pire des cas.
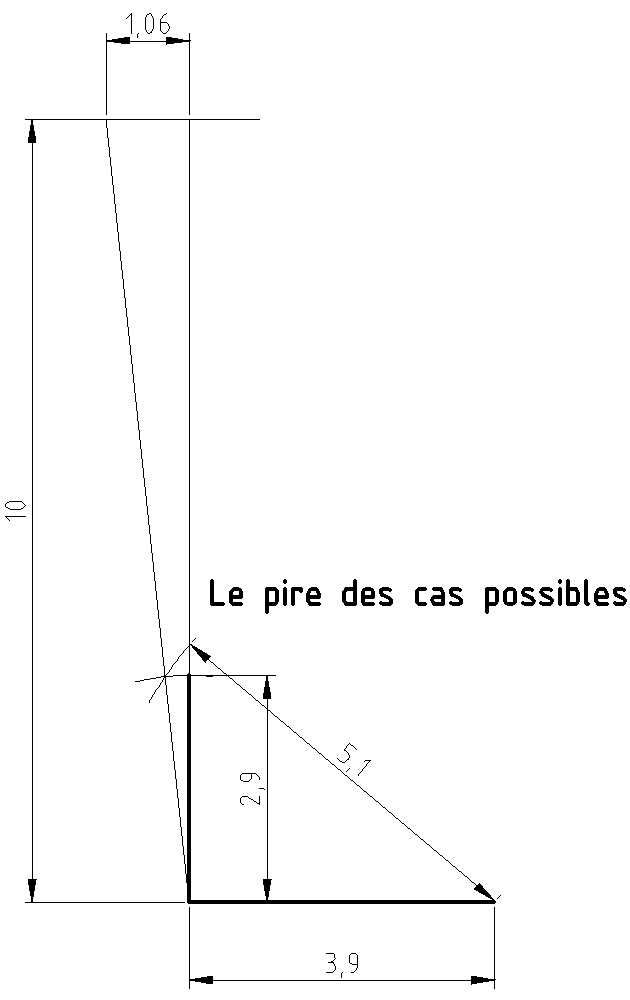
On envisage ici une erreur de mesure de 10cm en moins sur les 2 cotés de l'angle droit et 10 cm en plus sur l'hypoténuse.
Bien sûr cette erreur est monstrueuse, mais elle permet de faire un dessin qui montre bien les choses et elle est suffisament faible pour qu'on puisse faire une interpolation linéaire vers des valeurs plus raisonnables. Sur le dessin, l'erreur est de pratiquement 1m au bout de 10m. Avec des erreurs plus réalistes de 5mm, soit 20 fois moins, la dérive serait tout de même de 5cm au bout de 10m et donc de 6cm au bout de 12m.
Si on dispose d’un décamètre, on prendra 2m comme unité ; les erreurs seront divisées par deux.
Si on dispose d'un triple mètre, le triplet 20 , 21 , 29 sera idéal avec 2m, 2.10m et 2.90m. Pour un mètre à ruban de 5m on multipliera ces valeurs par 1,7. Le mien fait 8m. Je pourrais utiliser un facteur 8 / 2.9 = 2,758 ou plus raisonnablement 2,7.
***** © M Guignard *****

Comments powered by CComment