Comment déterminer la hauteur d’une fuite

Il arrive parfois que le liner de votre piscine se perce ou se fende. La réparation ne présente pas de difficulté en soit ; le problème est de situer la fuite.

Le présent article donne une méthode pour situer cette fuite en hauteur ce qui limitera le champ de recherche.

Je donne ici le cheminement complet du calcul pour les curieux. Les autres pourront se contenter d’appliquer la procédure donnée en fin d’article, munis d’une calculette, ou utiliser un tableur Calc, Excell ou autre.

Mais les calculs ne sont qu’une partie des difficultés qui nous attendent...

A -La décharge d’un condensateur

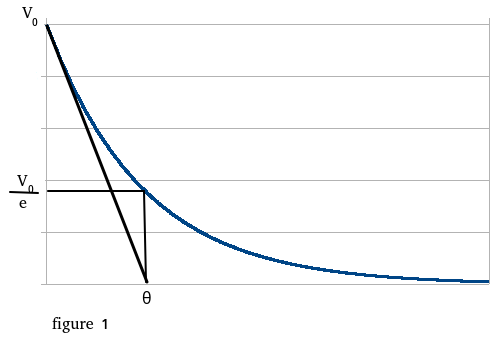
Pour ceux qui sont un peu familiarisés avec les circuits électronique, je rappelle comment se fait la décharge d’un condensateur dans une résistance. On verra ensuite que le vidage d’une piscine est un processus physique similaire.

Quand on décharge un condensateur dans une résistance, à chaque instant le courant est égal à V / R . V est la tension aux bornes du condensateur et de la résistance. À mesure que le condensateur se décharge, le courant diminue et la décharge devient de plus en plus lente.

Les calculs font intervenir la valeur θ = R × C appelée constante de temps du circuit. Si la décharge se maintenait telle qu’au premier instant elle serait terminée au bout du temps θ. En réalité, au bout de ce temps, il reste V₀ / e.

V₀ est la tension initiale et e est le nombre d’Euler, un de ces nombres magiques qui apparaissent en maths.

On a e = 2,71828…

Au bout de 2θ il reste V₀ / e^2 qu’on écrit plutôt V₀ × e^-2.

L’équation de la décharge s’écrit V = V₀ e^-t/θ.

Tout ceci est illustré par la figure 1.

B - La vidange d’une piscine

Lorsqu’on vidange une piscine en ouvrant un orifice tout en bas, le processus est identique à la décharge du condensateur. En effet, ce qui fait sortir l’eau c’est la pression due au poids de l’eau au-dessus de l’orifice. Cette pression est proportionnelle à la hauteur d’eau au-dessus de l’orifice. Plus le niveau baisse, plus la pression faiblit et donc plus le débit s’atténue. Ainsi, si la hauteur d’eau initiale est de 1,20m et qu’au bout de 20mn on est à 60cm, on divise la hauteur par 2 toutes les 20mn. Au bout de 40mn il reste 30 cm , au bout d’une heure 15 cm etc..

Précisons que le facteur 2 évoqué ci-dessus correspond sensiblement à 0,69 fois la constante de temps. Il convient de bien comprendre qu’à chaque constante de réduction correspond un certain nombre de fois la constante de temps.

C -La procédure de détection

La perte d’eau par une fuite s’apparente à une vidange. La seule différence est la hauteur de l’orifice. Supposons que l’on ait une fente 50cm en dessous du niveau initial. Le premier jour, on perd 5cm. On voit qu’à ce rythme il faudrait 10 jours avant que les choses se stabilisent 50cm plus bas. La constante de temps serait donc d’environ 10 jours. En réalité, au bout de ce temps il nous restera 50 / e = 18,4 cm d’eau au-dessus du point de fuite.

Bon, mais dans la vraie vie, on ne connaît pas cette donnée de 50 cm, c’est même ce que l’on cherche ! Pour le déterminer on va situer 3 points sur notre courbe de vidage. C’est la variation de la perte de hauteur sur 2 intervalles de temps égaux qui va nous donner la solution.

C.I -Les relevés

Le premier jour J₀, on mesure soigneusement la hauteur d’eau depuis le fond (ou depuis le rebord) de la piscine. Niveau N0_.

Le deuxième jour J₁, à la même heure on refait une mesure identique. Niveau N1

Idem pour J₂ . Niveau N2.

NB : On peut aussi faire les relevés depuis le dessus de la piscine puisque ce qui comptera en définitive c’est les écarts de niveaux. On fait reposer sur le bord une latte assez longue. On fixe en permanence un réglet perpendiculairement à la latte pour qu’il trempe largement dans l’eau. On repère à chaque fois la graduation à l’interface air/eau.

On note h1 la distance entre No et N1 et h2 la distance entre les niveaux N1 et N2.

Ceux qui n’aime pas les maths peuvent sauter ceci :

C.II -Les calculs

NB : Dans les calculs, les puissances sont notées avec le signe ^. Par exemple a^-2 signifie a puissance -2 qu’on pourrait écrire a^-2 nettement moins lisible, surtout le signe moins.

On a :

N0 = H hauteur initiale au-dessus de la fuite.

N1 = H e^-n où n correspond à un certain nombre de fois la constante de temps.

N2 = H / e^-2n. On a doublé le temps.

Dans la suite, h1 est la hauteur perdue le premier jour ; h2 est la hauteur perdue le jour suivant. Mais on pourra être amené à remplacer l’intervalle de 1 jour par 2 jours ou plus. Ce qui compte c’est de bien garder le même intervalle pour h1 et h2.

h1 = N0 – N1 = H – H e^-n = H (1 – e^-n) (1)

h2 = N1 – N2 = H e^-n - H e^-2n = H( e^-n - e^-2n ).

On en déduit,

h1 / h2 = (1 – e^-n) / e^-n - e^-2n = (1 – e^-n) / e^-n (1 - e^-n )

En simplifiant par (1 – e^-n ) on obtient h1/h2 = 1 / e^-n = e^n.

Ici, l’astuce consiste à passer aux logarithmes népériens. Ce qui nous donne :

ln(h1) – ln(h2) = n (2)

dans (1) en remplaçant n par sa valeur, on déduit H:

H = h1 / (1 – e^-n) (3)

Ceux qui n’aime pas les maths peuvent reprendre ici ou passer directement au tableur:

Donnons un exemple :

NB : Si vous n’êtes pas très à l’aise avec ces calculs, je vous conseille de suivre l’exemple. Vous remplacerez ensuite les valeurs proposées par les vôtres.

Supposons qu’on mesure une perte h1 = 50mm au bout d’un jour et h2 = 39 mm de plus le jour suivant.

On calcule les logarithmes de 50 et de 39. Pour cela il faut une calculatrice en mode scientifique. Vous devriez avoir une touche notée ln. On tape 50 puis on appuie sur la touche ln , puis touche – (moins) , 39 , ln , =.

on obtient n = 0,2484...

de (3) on va tirer H = h1 / (1 – e^-0,2484) .

On calcule d’abord e^ -0,2484.

Pour cela on passe sur les fonctions inverses . La touche qui fait cela s’appelle 2ndr chez Microsoft et majuscule sur Kcalc, l’une des calculatrice de Linux. À vous de vous adapter.

Tapez la touche « +/- » de changement de signe puis ex . On obtient 0,78

On appuie à nouveau sur la touche « + / - » pour avoir – e^-0,2484 et on ajoute 1 ce qui nous donne 0,22 . On appuie sur la touche 1/x (parce que diviser par x revient à multiplier par 1/x) on obtient 4,5454 et pour finir on multiplie par 50.

On obtient 227,2. La fuite se situe 227mm en dessous du niveau N0.

C.III -Un tableur pour faciliter les calculs

Je vous propose de créer un tableur avec Calc de LibreOffice ou Excel ou un autre en ligne, qui vous permettra de faire des essais instantanément.

Vous pouvez aussi en trouver un tout prêt un peu plus loin.

Sur la première ligne vous écrivez de A à F : h1 ; h2 ; ln(h1) ; ln(h2) ; n ; H ; intervalle ;h1/h2 ; incertitude .

En A2 : 50; En B2 : 39 (les valeurs de l’exemple ci-dessus).

En C2 (sans oublier le signe =) : =LN(A2) ; et la suite : =LN(B2) ; =C2 – D2 ; =A2/(1-EXP(-E2)) . Vous lisez la valeur H = 227 dans la colonne F.

En H2 écrivez = a2/b2. En I2 notez la valeur de l’incertitude des relevés (voir la suite).

En A3 : ==A2+2*$I$2; en B3 : =B2-2*$I$2 ; en A4 = A2-2*$I$2 ; en B4 : =B2+2*$I$2

Sélectionnez de A3 à B4 > clic-d > style > accent 2.

Sélectionnez de A2 à B4 et tirez le petit carré vers le bas jusqu’à la ligne 19.

Sélectionnez de C2 à F2 et tirez vers le bas jusqu’à la ligne 19.

En G4 : =F4-F3. Sélectionnez de G2 à G4 et tirez vers le bas jusqu’à la ligne 19.

Sélectionnez H2 et tirez vers le bas jusqu’à la ligne 19.

C’est tout, votre tableur est prêt. Il proteste sur les lignes où h1 et h2 ne sont pas encore renseignés. C’est normal n’en tenez pas compte. Vous n’avez plus qu’à placer des valeurs correspondant à h1 et h2 dans les colonnes A et B uniquement dans les cellules blanches et vous aurez instantanément en colonne F les valeurs de la profondeur du trou pour les différentes valeurs de h1 et h2 envisagées.

Pour les paresseux voici le tableur tout fait.

Le tableur

D -Considérations sur la précision

Les physiciens vous le dirons tous, une mesure ou un calcul n’ont de valeur qu’accompagnés de leur marge d’erreur.

Essayons :

Le repérage d’un niveau ne peut guère être plus précis qu’à 0,5mm près en plus ou en moins. Voyons le pire des cas  à propos de notre exemple:

Les vrais niveaux sont par exemple 1000    950    911

Les valeurs relevées sont 1000,5    949,5    911,5

Ce qui nous donne pour h1 et h2, 51 et 38mm au lieu des valeurs vraies 50 et 39.

Les erreurs de repérage sont telles ici qu’elles augmentent h1 de 1mm et diminue h2 de 1mm ce qui n’est pas sans conséquences. Essayez avec le tableur en écrivant 0,5 en I2 ; 50 en A2 et 39 en B2.

Les calculs donnent bien 227 en F2 mais aussi 200mm en F3 pour h1 = 51 lu en A3 et h2= 38 lu en B3. Soit un écart de 27mm. Ce qui n’est pas catastrophique.

Mais ce n’est pas tout. On peux faire les erreurs en sens inverse. Dans ce cas (le pire) on a h1 = 49mm et h2 = 40 mm (ligne 4). Cette fois-ci on situe la fuite à 267mm (vérifiez avec le tableur). Entre les extrêmes on devrait inspecter une bande de 267- 200 = 67 mm (lire en G4) ce qui est reste acceptable. Mais remarquez que les mesures sont supposées très soigneuses.

Toutefois dans la réalité les choses sont un peu différentes. On ne sait pas à priori si on est tombé près du premier cas, ou du 2ieme ou ou du 3ieme ou ailleurs.

Envisageons chaque cas.

• Premier cas, les mesures sont parfaites. Comme on ne le sais pas on va faire exactement les calculs ci-dessus et situer la bande à explorer entre 200 et 267mm.

• Deuxième cas on a trouvé h1 = 51mm et h2 = 38 mm (à écrire ligne 5). Ce qui nous placerait à 200mm

On va envisager 2 cas :

• h1 = 50mm et h2 = 39 mm (à lire ligne 7) ce qui donne la vrai position de la fuite à 227mm. Mais on ne le sais pas !

• h1 = 52mm et h2 = 37 mm (à lire ligne 6) ce qui nous amène à 180mm. On va chercher la fuite entre 227 et 180mm soit sur un intervalle de 47mm affiché en G7.

• Troisième cas on a trouvé h1 = 49 et h2 = 40mm ce qui nous place à 267mm

On envisage 2 cas

• h1 = 50mm et h2 = 39 mm ce qui donne la vrai position de la fuite à 227mm.

• h1 = 48 et h2 = 41 ce qui nous amène à 329mm. Il faudra parcourir une bande de 102mm comme indiqué en G10. Ça devient limite.

Remarquons que le rapport h1 / h2 relevé (donné colonne G du tableur) est de 49 / 40 = 1,225. Disons que toute mesure donnant un rapport h1/h2 inférieur à 1,25 sera à exclure.

Une autre difficulté est à considérer : l’évaporation. Elle peut facilement atteindre 5mm et parfois dépasser 1cm. Elle ne doit donc pas être négligée.

E -Solutions aux différents problèmes

E.I -L’évaporation

On pourra pendre au rebord de la piscine, un petit seau rempli d’eau, avec quelques cailloux au fond. Ainsi les températures de l’eau de la piscine et du seau seront égales et donc les conditions d’évaporation identiques à condition que les bords du seau ne dépassent pas trop (sinon la circulation de l’air dans le seau et dans la piscine ne seront pas les mêmes). On devra relever le niveau d’eau dans le seau pour voir de combien il a baissé par évaporation. Cette baisse devra être retirée de h1 et h2 (et doublera les incertitudes !).

Toutefois, les baigneurs placent souvent une bâche à bulle sur l’eau pour retenir la chaleur et les saletés. Dans ce cas, il n’y a plus d’évaporation (ou elle est négligeable). C’est LA solution retenue pour la suite.

E.II - Incertitude sur les niveaux

E.II.a -Augmenter artificiellement h1 et h2

Si on incline l’instrument de mesure d’un angle de a° par rapport à l’horizontale, pour une variation de niveau h, l’interface air-eau parcourra une longueur l = h / sin(a). Par exemple pour 30° on a sin(30°) = 0.5 donc : l = 2h. Ainsi l’incertitude de plus ou moins 0,5mm sera 2 fois moindre en valeur relative.

Attention, la valeur H calculée devra être divisée par 2.

En pratique on pourra opérer ainsi (figure 2).

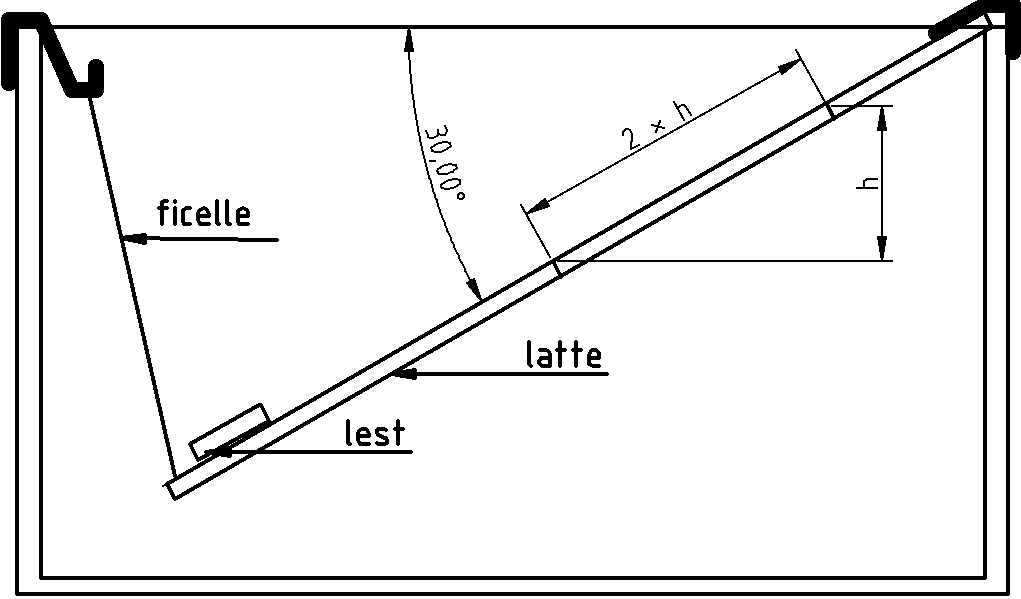                                  figure 2

On place une latte, ou un profilé métallique, suivant une corde (je suppose la piscine circulaire, sinon utiliser un angle), en accrochant une extrémité au rebord de la piscine et l’autre extrémité soutenue par une ficelle à la profondeur adéquate. Si on utilise une latte en bois il faudra évidemment la lester. On fixe sur la latte un réglet avec sa graduation 0 au raz de l’eau ou un peu au-dessus. La position exacte n’a pas d’importance puisqu’on fonctionne sur des différences.

E.II.b -Améliorer la précision

Je vous propose un petit dispositif pour réduire le 1/2mm d’incertitude.

Prenez une latte d’au moins 1m de long. Au milieu, percez (de préférence à la perceuse à colonne) un trou de diamètre 10mm.

Introduisez à force dans ce trou un manchon taraudé (comme un écrou mais beaucoup plus haut) à D= 6mm.

Vissez une tige filetée dans le manchon.

À une extrémité de la tige filetée, vissez un écrou sur 1cm environ, passez une rondelle large et vissez un autre écrou. Serrez.

Votre outil est prêt. Il s’utilise de la façon suivante.

Posez la latte sur le rebord de la piscine de façon à ce que la tige filetée soit verticale à quelque cm du bord, les écrous en haut. Introduisez une clé à pipe sur l’écrou du haut et vissez, rapidement au début, puis très lentement quand vous approchez du contact de la tige avec l’eau. Arrêtez dès que ça touche. Vous êtes au niveau N0.

Le lendemain, placez la clé à pipe face à vous et vissez en comptant les tours jusqu’au contact. Faites votre comptage à 1/8 de tour près (45°). Comme le pas de la tige filetée est de 1mm vous obtenez directement h1 à 0,125mm près (théoriquement).

Faites de même pour h2.

Dans les calculs d’incertitude, vous remplacez le 1/2 mm d’écart par 0,25mm en I2 dans le tableur, pour vous garder une marge. À condition qu’il n’y ait aucune ondulation à la surface de l’eau !

Reprenons l’exemple précédent :

Dans un monde idéal, vous auriez obtenu h1 en vissant exactement 50 tours et h2 en 39 tours.

En réalité vous pouvez avoir fait 50,5 et 38,5 tours, ou bien 49,5 et 39,5.

Le premier cas situe la fuite à 212,5mm

Le 2em cas (le pire) situe la fuite à 245mm (vérifiez avec le tableur). Entre les extrêmes on devrait inspecter une bande de 245-212= 33mm.

E.II.c -Prolonger les mesures dans le temps

Si les valeurs de h1 et h2 sont trop proches sur un intervalle de 1 jour, on peut fonctionner sur des tranches de 1,5 jour en faisant des relevés par exemple à 9h au jour J puis à 21h le lendemain puis à 9h à j +3. Pour les fuites lentes et à grande profondeur, on serra amené à travailler sur des intervalles de 2 jours ou davantage.

Envisageons quelques cas :

Pour cela nous allons utiliser un autre tableur ou plus exactement une autre zone de notre tableur :

En B20 écrivez hauteur . En A21 écrivez  temps  ; en C21 écrivez perte.

En A22 écrivez 0 et en dessous 0,01. Sélectionnez A22 et A23 et tirez la croix vers le bas jusqu’à la ligne 222 au moins.

En B21 écrivez 50. Sur cette cellule, faites un clic-d > style > choisissez un style qui ressort bien, accent 3 ou erreur par exemple.

En B22 écrivez =$B$21*EXP(-A22) et tirez vers le bas.

En C23 écrivez =$B$21-B23 et tirez vers le bas.

Explications :

B21 donne la profondeur de la fuite à l’instant 0.

La colonne A donne des temps en nombre de fois θ par pas de 0,01θ.

La colonne B donne la hauteur d’eau restant au-dessus de la fuite à l’instant correspondant.

La colonne C indique la baisse de niveau depuis l’instant 0.

Étudions quelques cas :

La fuite est à 50mm  :

On écrit 50 en B21.

perte 20mm (à un poil près) à 0,52θ ; 30mm à 0,92θ ; 40mm à 1,61θ (le rapport des temps pour doubler les pertes de 20 à 40mm r20-40 = 1,61/ 0,52 = 3,1. On perçoit bien la non linéarité de la courbe. Le résultat des calculs sera très bon.

fuite à 100mm

On écrit 100 en B21

* perte h1 = 20mm à 0,22θ.

On double le temps t=0,44. La perte totale est de 36. La perte h2 est de 16 (36-20). Le couple avec erreurs 19,5 et 16,5 (à reporter dans le premier tableur) nous donne H=127. Correcte si l’incertitude des niveaux est effectivement de 0,25mm.

* h1=30mm à 0,36θ .

On double le temps t=0,72. La perte totale est de 51. La perte h2 est de 21. Le couple avec erreur de 1mm, 29 et 22 nous donne H=120. Ok. On a h1 / h2 = 1,32.

fuite à 200mm

On écrit 200 en B21

h1=19mm à 0,10

Si on double le temps, on double sensiblement la perte, on ne perçoit pas la non linéarité de la courbe ; il faut aller voir nettement plus loin.

h1 =39,5mm à 0,22θ. À 0,44θ la perte totale est de 71,2. La perte h2 est de 32. Le couple avec erreur (système avec tige filetée) 39 et 32,5 nous donne H=234. Ok. h1/h2 = 1,22.

fuite à 500mm

On écrit 500 en B21

On a h1 = 19,6mm à 0,04θ.

* Si on multiplie le temps par 2 on est à 38,4 h2= 18,8 soit h1/h2=1,04. Trop proche de 1 !

* Si on multiplie le temps par 4 (0,16θ) on est à 74mm de perte. En doublant ce temps (0,32θ) on passe à 137mm donc h2 = 63mm. Avec les pires erreurs on a h1 = 73,5 et h2 = 63,5 ce qui nous situe la fuite à 540mm. h1 / h2 = 1,16.

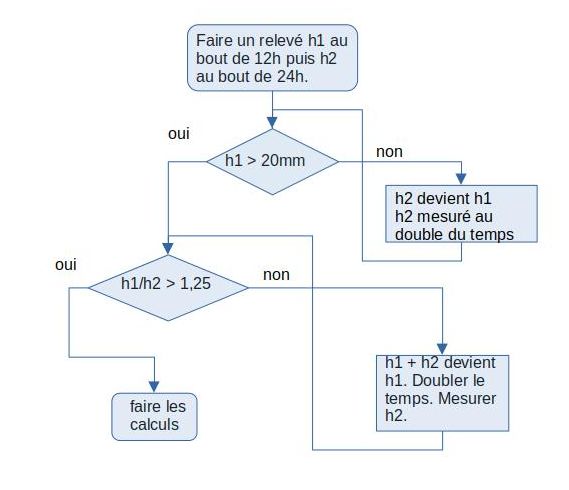
F -Comment procéder

Au départ, on ne connaît ni la profondeur de la fuite ni son importance. Une perte rapide peut correspondre à une grande fente à faible profondeur ou à un « petit » trou à grande profondeur.

Les calculs ci-dessus montrent qu’il faut relever h1 au bout d’au moins 0,15θ, mais on n’a pas la moindre idée de la valeur de θ à priori.

Ne perdons pas de vue que h2 doit être relevé exactement au double du temps pris pour h1 (les calculs donnés en CII reposent sur cette hypothèse).

On procédera suivant cet organigramme:

G -Conclusion

La méthode décrite dans cet article peut rendre service mais elle ne fait pas de miracle.

Notez en particulier que plus la fuite est profonde, plus il faudra accepter de perdre de l’eau, d’une part parce-qu’une valeur de h1/h2 donnée (voir calculs en CII) correspond à une plus grande hauteur d’eau, et d’autre part parce que pour une zone à explorer donnée l’erreur relative est inversement proportionnelle à la profondeur initiale. Ainsi, au-delà de disons 200mm, le critère h1/h2 > 1,25 devient insuffisant.

***** copyright M Guignard 2022 *****