Les marées, comment ça marche ?

Les marées, sont dues à la lune qui attire l'eau des océans. C'est du moins ce que la plupart des gens pensent. Pas si simple !

En effet, il y a environ deux cycles de marées par jour, et si l'on comprend que la mer se soulève en face de la lune, on a plus de mal à comprendre qu'elle se soulève simultanément du coté opposé. Alors reprenons.

D'après la théorie de la gravitation de Newton, la Terre et la Lune s'attirent mutuellement avec la même force.

Pourquoi la Lune ne tombe t-elle pas sur la Terre ?Parce qu'elle tourne autour de la terre et la force centrifuge compense l'attraction terrestre. OK.

Mais la Lune attire la Terre. Pourquoi la Terre ne tombe t-elle pas sur la Lune ? Eh bien parce que la Terre tourne autour ... de la Lune ?

Ah, Ah ! Qui tourne autour de qui ? En fait, La Terre et la Lune tournent toutes deux autour d'un même point G, qui est le centre de masses de l'ensemble. Il n'est pas question de s'étendre ici sur la définition du centre de masse disons juste que celui-ci se situe sur la ligne qui joint les centres des deux objets célestes et que la Terre étant environ 81 fois plus massive que la Lune, G se trouve 81 fois plus près de la Terre que de la Lune. Ainsi le centre de la Terre décrit un cercle (en réalité une ellipse mais très peu aplatie) 81 fois plus petit que celui de la lune. Ce qui importe c'est qu'elle tourne et donc qu'il y ait une force centrifuge qui empêche la Terre de tomber sur la Lune.

Le point G est à l'intérieur de la Terre, à environ 4680 km du centre.

Le rayon de la Terre est de 6400km. La distance Terre Lune de 384000km.

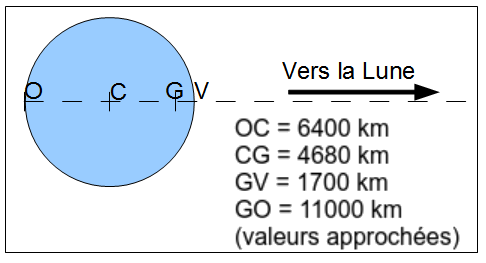
Globalement, la force centrifuge équilibre exactement l'attraction lunaire. Mais on peut considérer la Terre comme un ensemble de masselottes agglutinées les unes aux autres.

• Pour une masselotte au centre C de la Terre, les forces se neutralisent exactement.

• Pour une masselotte placée coté  Lune, en V, l'attraction lunaire s'ajoute à la force centrifuge. La résultante est dirigée du coté opposé à C et soulève l'eau des océans.

• Pour une masselotte à l'opposé de la Lune, en O, l'attraction lunaire est dirigée vers le centre de la terre et s'oppose à la force centrifuge qui est plus forte car O est nettement plus éloigné de G. La force résultante soulève donc aussi l'eau des océans.

Voyons ça de plus près.

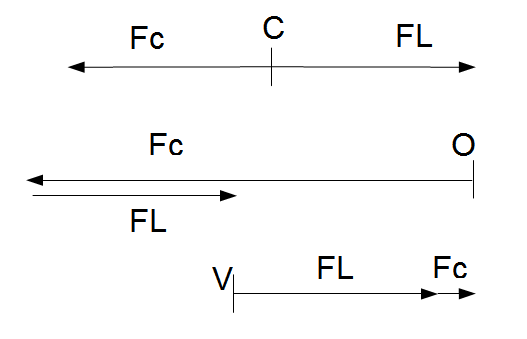
En C les forces sont opposées et égales en grandeur F_c = F_L

_où F_c est la force centrifuge en C et F_L l'attraction lunaire.

Comme la force centrifuge est proportionnelle au rayon du cercle décrit, on la représente par un vecteur de longueur 47mm dirigé vers la gauche. Donc F_L fait aussi 47mm mais dirigé vers la droite.

En V la force centrifuge est représenté par une longueur de 17mm seulement dirigée vers la droite. Pour l'instant on suppose que l'attraction lunaire reste identique. La résultante mesure 47 + 17 = 64mm.

En O la force centrifuge est représentée par une longueur de 111mm dirigée vers la gauche. La résultante s'obtient en retranchant les 47mm de F_L . Elle mesure donc 111 – 47 = 64 mm comme en V. Elle est dirigée vers la gauche donc vers l'extérieur à la Terre.

En réalité, l'attraction lunaire n'est pas constante. Corrigeons notre approximation.

Le rayon de la Terre étant très petit devant la distance Terre Lune, on peut calculer les variations en termes de pourcentages . En passant de C à V, on réduit la distance d'environ 1,7% ; on augmente donc l'attraction de 3,4% car elle varie avec le carré de la distance(rappel : ( 1+ ε)² ≈ 1 + 2ε) . En passant de C à O on diminue l'attraction de 3,4%. Ainsi on doit raccourcir l'attraction lunaire du coté où elle s'oppose à la force centrifuge et la rallonger de la même quantité du coté où elle s'ajoute. En définitive, les deux forces de marées restent égales, elles sont juste un tout petit peu plus fortes que ce qui avait été dit initialement.

J'ai expliqué les choses avec les valeurs particulières du couple Terre Lune. Les plus matheux pourrons reprendre les calculs en raisonnant avec R pour le rayon et d pour la distance GV. Ils verront que ça marche à tous les coups.

C'est ainsi que les forces de marée tirent sur les objets satellisés 'par les deux bouts' et parviennent parfois à les briser.

En réalité, les phénomènes de marée sont beaucoup plus complexes. L'inertie de l'eau et le profil des côtes, interviennent entre autres choses, dans le rythme de propagation des marées, ainsi que des phénomènes de résonances. De plus, le soleil combine plus ou moins son effet à celui de la Lune. C'est ce qui explique les fluctuations de l'amplitude des marées avec les lunaisons et les grandes marées d'équinoxes.

    ****** © M Guignard  *****