Dans le ciel, comment tournent les objets célestes ?

Si on observe le ciel pendant plusieurs heures d'une même nuit, on constate que les étoiles tournent d'est en ouest, comme le soleil de jour. Voyons ce qu'il en est exactement.

A -Pourquoi ça tourne ?

Le fait est bien connu, ce n'est pas le ciel qui tourne mais la Terre qui tourne sur elle- même. Malgré tout, nous dirons ici que le ciel tourne, puisqu'il s'agit de parler de ce que nous voyons. Ce qu'il faut retenir, c'est que l'axe de rotation est celui de la Terre : une grande ligne droite allant du pôle nord au pôle sud en passant par le centre de la Terre. Cette ligne peut être prolongée jusqu'au ciel. Comme la Terre est très petite comparée aux distances astronomiques, nous pouvons déplacer l'axe parallèlement à lui-même pour le faire passer par nos pieds, où que nous soyons sur Terre.

Puisque nous parlons de ce que nous voyons, nous pouvons considérer le ciel comme un immense chapiteau de forme sphérique(la sphère céleste), qui tourne suivant l'axe de la Terre et dont nous occupons le centre, où que nous soyons ¹. Les étoile sont piquées dans la toile du chapiteau. Le sol sur lequel nos pieds reposent peut, être assimilé à un plan. Ce plan contenant le centre de la sphère, il la coupe en deux parties égales, l'une au-dessus qui est visible, l'autre en dessous, qui est cachée. À un instant donné, nous ne voyons qu'une moitié du ciel.

B -Où est l'axe ?

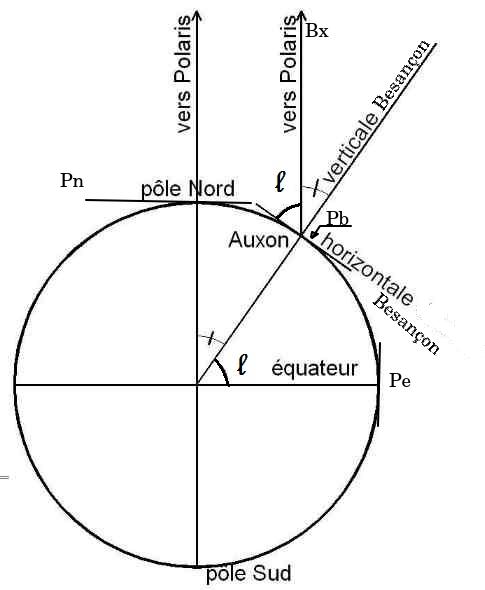  Considérons la figure1 ci-contre qui représente une coupe de la Terre. Le plan de coupe contient le pôle nord, le pôle sud et Besançon. La latitude l de Besançon est de 47°. Pb est le plan tangent à la Terre  à Besançon, c'est le plan évoqué au paragraphe précédent. Bx est l'axe de rotation de la terre, translaté à Besançon. Quelques considérations géométriques simples nous permettent d'affirmer que la droite Bx fait avec le sol un angle de 47° égal à la latitude de Besançon. Au pôle nord, le plan Pn est perpendiculaire à l'axe et à l'équateur, le plan Pe est parallèle à l'axe translaté Ex.

Ainsi, à Besançon, il faut imaginer l'axe comme sortant du sol entre nos pieds pour s'élever en direction du nord, suivant une ligne inclinée de 47° par rapport au sol. L'extrémité de cette ligne est matérialisée dans le ciel par l'étoile polaire.

Pour une autre ville de France, les choses sont guère différentes : à Lille l'axe est incliné de 50° et à Perpignan de 42°.

C -La ronde des étoiles

Pour comprendre le mouvement des étoiles, les plus jeunes pourront s'aider d'un globe terrestre. Si on fait tourner le globe, on voit bien que Stockholm décrit un petit cercle, Paris un plus grand cercle, Tunis un cercle encore plus grand, etc. Par contre, tous ces cercles sont parallèles entre eux et situés dans des plans perpendiculaires à l'axe de rotation.

Revenons sur le terrain : les étoiles tournent autour d'un axe allant de nos pieds à l'étoile polaire, dans des plans inclinés de la latitude du lieu par rapport à la verticale (ou du complément de la latitude par rapport au sol). Celles qui sont proches du pôle nord céleste c'est à dire de l'étoile polaire, décrivent des petits cercles, elles montent et descendent peu et sont donc toujours visibles (dites circumpolaires). Certaines décrivent un cercle suffisamment grand pour venir tangenter la ligne d'horizon au nord. Les autres ont un lever coté est et un coucher coté ouest ². Les étoiles qui sont dans le plan de l'équateur terrestre, c'est à dire sur l'équateur céleste (voir le texte sur les coordonnées équatoriales) décrivent le plus grand cercle. Ce cercle, dont vous êtes le centre, passe par le point d'horizon est, le point d'horizon ouest et au sud, sa hauteur he est égale au complément de la latitude. Par exemple pour Besançon, he = 90 – 47 = 43°. Au-delà de l'équateur céleste, en continuant vers le sud, les cercles se rétrécissent à nouveau, le centre de rotation s'enfonce dans le sol et les étoiles montent de moins en moins haut. À partir d'une certaine limite, les étoiles ne sont jamais visibles.

Pour toutes les étoiles, la hauteur maximale est atteinte dans le plan méridien. Pour comprendre ce qu'est le plan méridien, imaginez un mur allant du nord au sud sur des km et montant … jusqu'au ciel !

Pour ceux qui auraient du mal à imaginer tout ça, je propose un petit bricolage.

Commencez par trouver une balle en mousse d'une dizaine de cm de diamètre. Vous pouvez aussi prendre une orange.

Plantez dans la boule, une aiguille à tricoter (ou un bâton de brochette), de part en part, en passant par le centre. Faites la ressortir suffisamment pour que la boule ne touche pas la table (mais presque) quand la pointe y repose et que l'inclinaison de l'aiguille est d'environ 45°.

Tracez l'équateur céleste : la ligne à mi distance des points d'entrée et de sortie de l'aiguille. Inscrivez une dizaine de lettres dans l'ordre alphabétique en allant du point d'entrée de l'aiguille (pôle nord) au point de sortie (pôle sud). Ce seront vos étoiles.

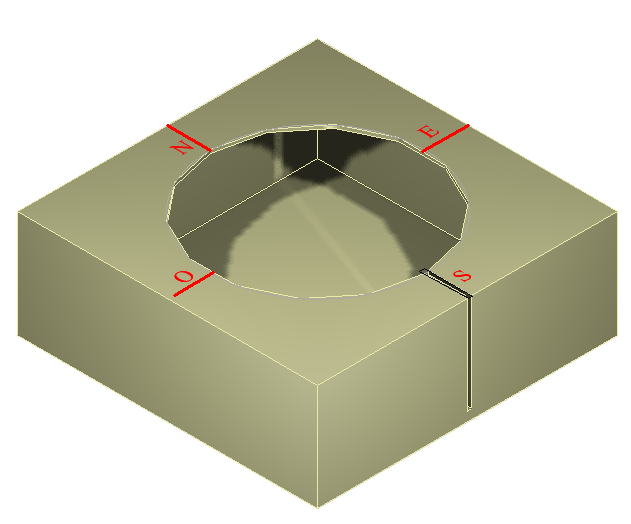Réalisez une boite en carton ayant pour cotés le diamètre de la boule, augmenté de 3 à 4 cm. La hauteur doit être égale à D/2 ou un peu plus. Découpez dans le dessus, un cercle de diamètre un peu supérieur à D. Le fond n'est pas indispensable(figure 2 ci-contre).

Marquez les directions nord, sud, est, ouest comme sur la figure 2. Faites une fente au sud.

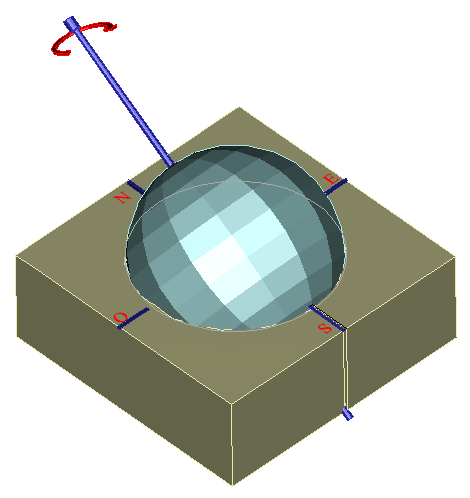
Vous n'avez plus qu'à introduire la boule dans la boîte. Inclinez l'aiguille de 45° environ et orientez la, nord sud comme sur la figure 3. Si la boule est à la bonne hauteur, l'équateur doit aller d'est en ouest, sinon faites coulisser la boule sur l'aiguille.

Faites tourner l'aiguille et constatez que certaines lettres restent toujours visibles et d'autres toujours invisibles : Un observateur français n'a pas accès à la totalité du ciel.                                                        

Vous devez faire un effort d'imagination : la surface de la boule représentant le ciel, l'observateur n'est pas censé être à l'extérieur mais au centre de la boule, qui est censée être creuse. La face supérieure de la boîte n'a pas d'équivalent dans la réalité, elle n'est là que pour matérialiser la ligne d'horizon de l'observateur qui correspond à la ligne de découpe circulaire. L'observateur ne voit du ciel que ce qui est au-dessus de cette ligne.

Vous pouvez également matérialiser le plan méridien en découpant un demi cercle du diamètre de la boule (ou légèrement plus) dans un rectangle de carton avec le centre au milieu d'un bord. Encastrez cette pièce sur la boule verticalement en l'orientant suivant la ligne N-S. Vérifiez que la trajectoire de chaque étoile est à son apogée au franchissement du plan méridien.

D -Et pour un Esquimau ?

Il est intéressant de se demander comment un habitant du pôle nord voit le ciel. Pour cela, redressez l'aiguille verticalement. Ajustez la position de la boule pour que l'équateur coïncide avec la découpe circulaire de la boîte. Faites tourner l'aiguille. Les étoiles tournent maintenant dans des plans horizontaux, elles ne montent et descendent jamais ; on voit toujours les mêmes. Ainsi, un observateur au pôle nord n'a accès qu'à une moitié du ciel, mais il y a accès à toute heure de chaque nuit. Les étoiles basses sur l'horizon, donc difficiles à observer le sont toujours. Notez que les indications N S E O n'ont ici pas de signification, au pôle nord, où qu'on aille on va au sud !

E -Et pour un Équatorien ?

Changez à nouveau l'inclinaison de votre aiguille : placez la horizontalement, sur les traits N et S. Vous êtes dans la situation d'un observateur situé à l'équateur (n'oubliez pas, vous êtes à l'intérieur de la boule, au centre). Les étoiles décrivent des cercles verticaux. Le ciel entier peut être vu, mais vous risquez de perdre facilement l'étoile polaire : elle est à raz de l'horizon. En contrepartie, il n'y a pas d'étoiles circumpolaires (visibles toute la nuit) ³.

F -On ne voit pas les mêmes étoiles en été qu'en hiver

C'est à cause de l'autre mouvement important de la Terre : sa révolution autour du Soleil. Mais ceci est une autre histoire...

1) Pour mesurer à quel point cette affirmation est justifiée, sachez que si la Terre était réduite à une bille de 1mm de diamètre, l'étoile la plus proche serait située à 3000km.

2. Noter que les étoiles circumpolaires se déplacent d'est en ouest (relativement au sol) quand elles sont plus hautes que l'étoile polaire, mais d'ouest en est dans le cas contraire.

3. En réalité, l'étoile polaire n'est pas tout à fait au pôle nord céleste. Elle décrit donc un petit cercle. Elle est donc tantôt un peu au-dessus de l'horizon et tantôt en dessous.

***** © Michel Guignard *****