Horaires de visibilité des Messiers
Le but de cet article est de fournir un outil permettant de savoir rapidement quels Messiers sont visibles à un instant donné.
La démarche est la suivante :
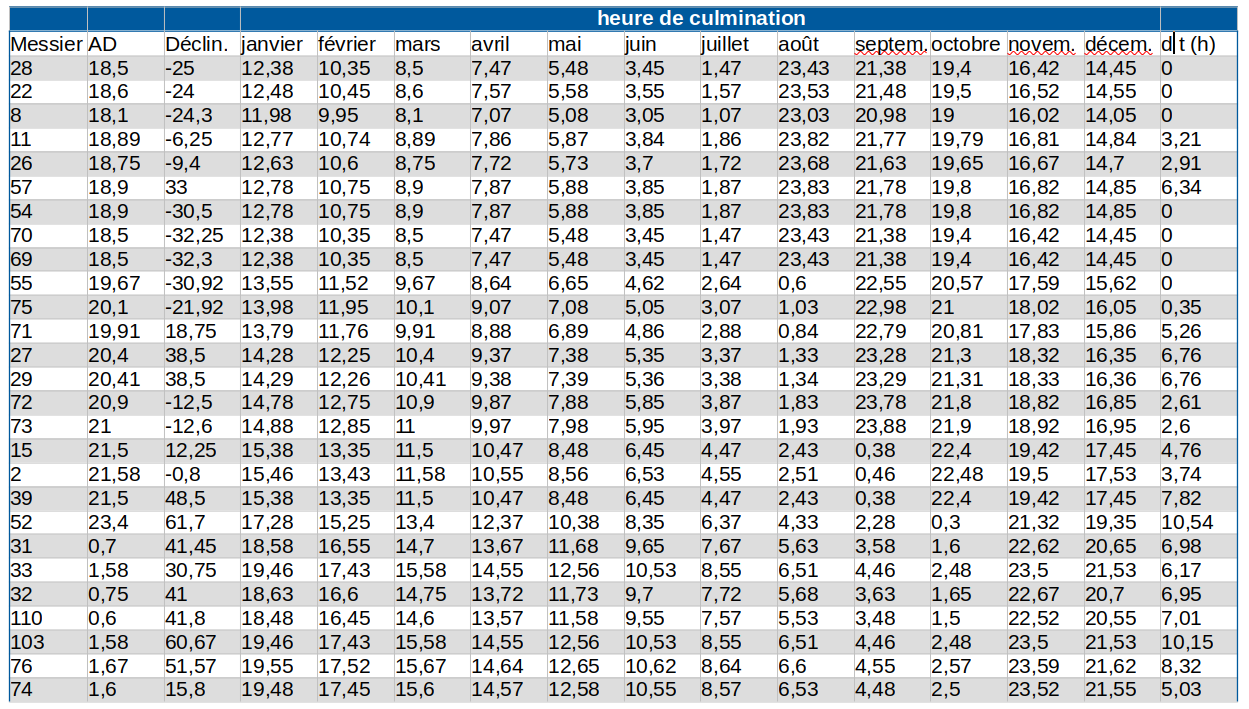
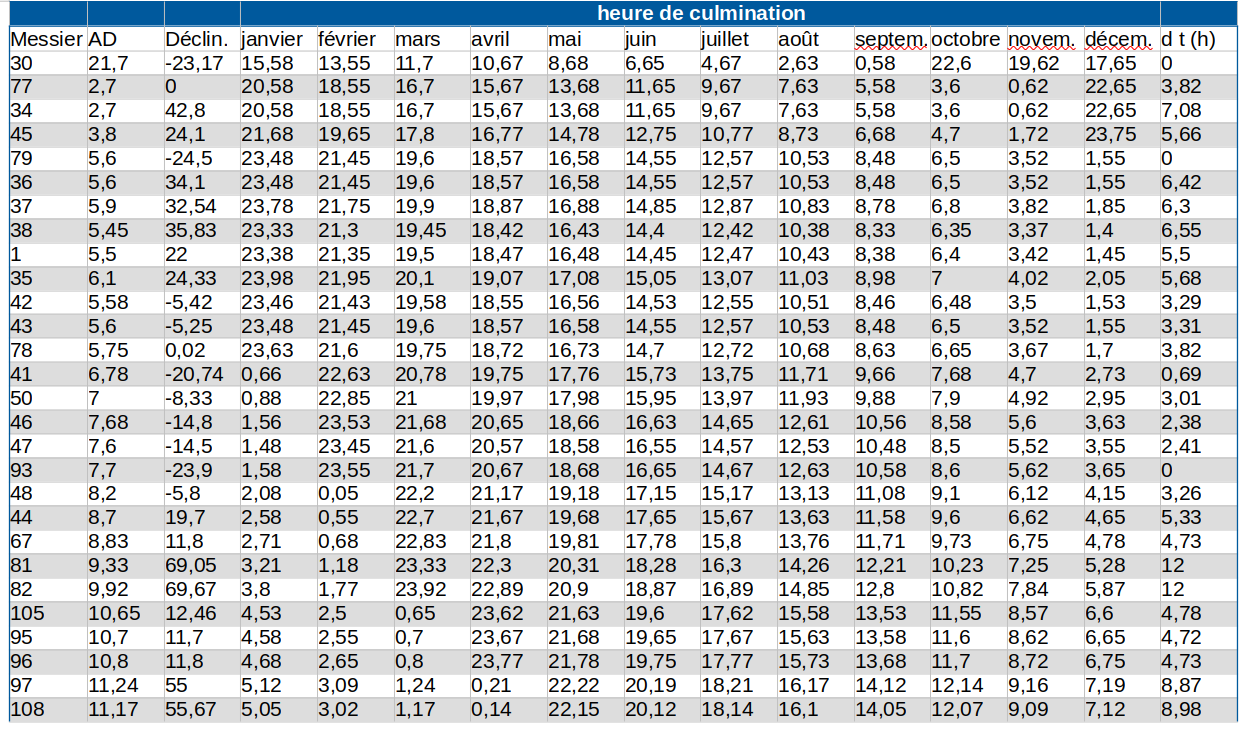
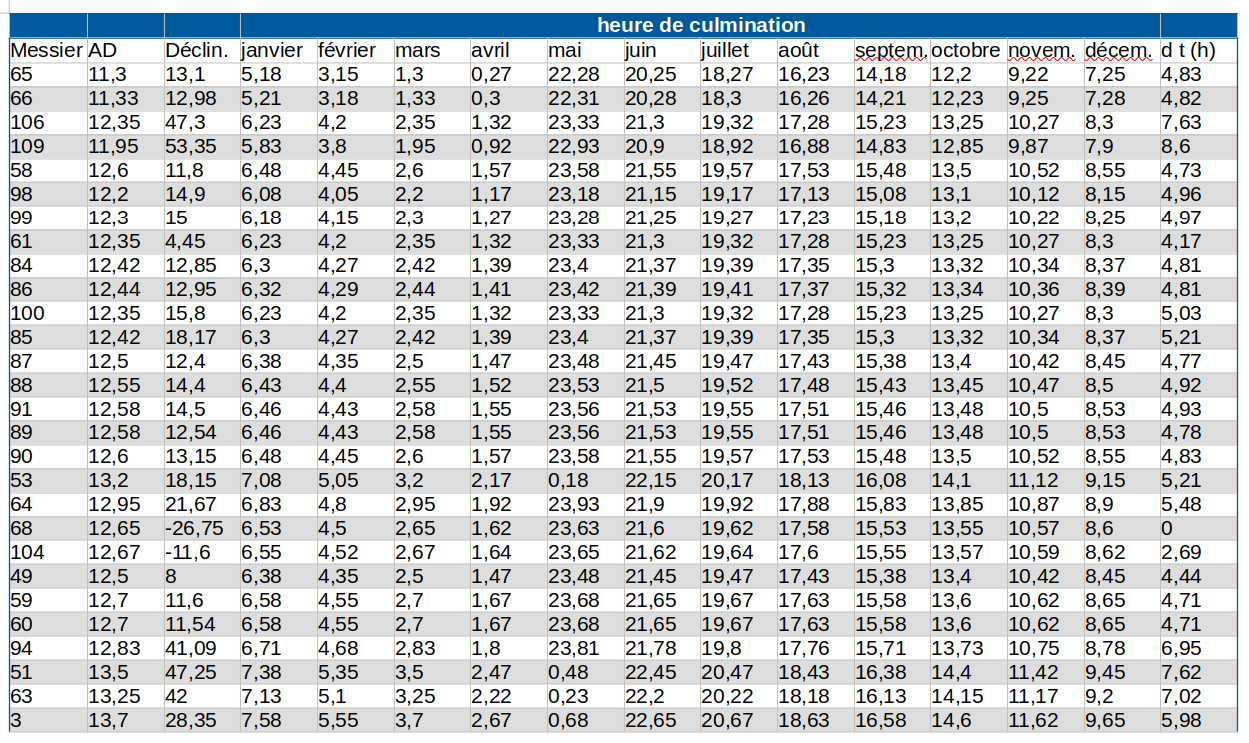
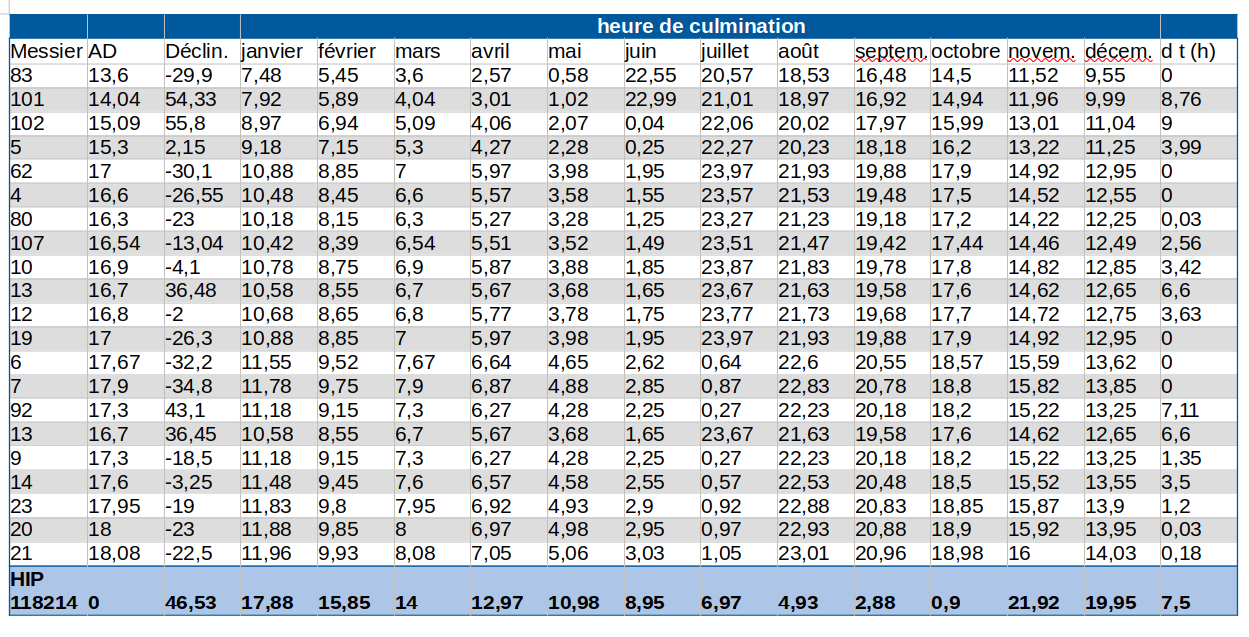
On donne, pour chaque objet, l’heure de culmination au premier de chaque mois. La dernière colonne donne l’intervalle de temps (avant ou après la culmination) où le Messier est visible. On entend par visible, situé à une hauteur supérieure à 20°. Un delta t de 0 ne signifie pas que l’objet n’est pas visible, mais qu’il ne le sera jamais dans de bonnes conditions. Tout ceci est calculé pour les environs de Besançon latitude et longitude environ 47°nord et 6°est. À chacun de faire les petites adaptations au lieu d’observation. Ou de refaire ses propres calculs suivant les indications données plus bas.
Voir en fin d'article le fichier pdf avec mise en évidence des périodes favorables.
Pour les curieux voici comment j’ai procédé.
A -Relevé des culminations de HIP 118214
J’ai choisi une étoile dont l’AD (ascension droite) est très proche de 0 : HIP 118124.
À l’aide de Stellarium, j’ai relevé les horaires de culmination en bloquant l’horloge et en faisant défiler les mois sur un an avec le jour fixé à 1.
J’ai trouvé, je ne sais plus où, une liste des Messiers classés plus ou moins par ordre d’AD.
B -Le tableau des heures de culmination par mois et des durées de visibilité
J’ai fait avec Calc le tableau ci-dessus. Les colonnes sont :
Numéro du Messier, son AD, sa déclinaison, heure de culmination en janvier, en février … en décembre, durée de visibilité avant ou après la culmination.
La cellule D3 contient : =MOD(D$107+$B3;24)
On fait la somme de l’heure de culmination de HIP 118214 en janvier ( en D107) et de l’AD du Messier concerné, car un objet d’AD H est en retard de H heures sur un objet d’AD 0. Si la somme dépasse 24h on ne doit garder que ce qui dépasse d’où l’usage de la fonction modulo.
On recopie pour tous les Messiers et tous les mois de l’année. 107 est précédé d’un $ car c’est toujours sur la ligne 107 qu’on lit la culmination de HIP 11824. B est précédé d’un $ car c’est toujours dans la colonne B qu’on lit l’AD du Messier.
C -La colonne des durées de visibilité
La dernière colonne est la plus difficile a remplir.
Il a fallu établir la courbe des durées de visibilité en fonction de la déclinaison. Pour cela j’ai encore utilisé Stellarium.
J’ai bloqué l’horloge.
J’ai choisi, pour chaque D (déclinaison) multiple de 5° (à 0,1° près), un objet quelconque dont j’ai noté l’heure de culmination. Puis j’ai fait tourner les heures en surveillant la hauteur. J’ai noté l’heure de passage à 20°.
Tout ceci donne le tableau suivant où on trouve pour chaque D l’horaire de culmination en deux colonnes, les heures (B) puis les minutes (C) ; l’horaire de passage à 20° en 2 colonnes aussi (D E). Ce qui permet de calculer les mêmes horaires en minutes colonnes (F G) et d’obtenir la durée en minutes colonne H (formule : =MOD(G2-F2;1440), puis en heures décimales (I) en divisant par 60.
A B C D E F G H I J
|
Déclin. |
culm H |
culm mn |
20° h |
20° mn |
T culm mn |
T 20° en mn |
delta T en mn |
delta h déci |
approxi. |
|
-22,5 |
23 |
18 |
23 |
32 |
1398 |
1412 |
14 |
0,23 |
0,18 |
|
-15 |
12 |
23 |
14 |
45 |
743 |
885 |
142 |
2,37 |
2,37 |
|
-10 |
8 |
16 |
11 |
17 |
496 |
677 |
181 |
3,02 |
2,85 |
|
-5 |
6 |
15 |
9 |
46 |
375 |
586 |
211 |
3,52 |
3,34 |
|
0 |
17 |
23 |
21 |
19 |
1043 |
1279 |
236 |
3,93 |
3,82 |
|
5 |
22 |
32 |
2 |
53 |
1352 |
173 |
261 |
4,35 |
4,21 |
|
10 |
3 |
32 |
8 |
17 |
212 |
497 |
285 |
4,75 |
4,59 |
|
15 |
7 |
22 |
12 |
27 |
442 |
747 |
305 |
5,08 |
4,97 |
|
20 |
12 |
20 |
17 |
47 |
740 |
1067 |
327 |
5,45 |
5,35 |
|
25 |
13 |
27 |
19 |
15 |
807 |
1155 |
348 |
5,8 |
5,73 |
|
30 |
18 |
22 |
0 |
31 |
1102 |
31 |
369 |
6,15 |
6,11 |
|
35 |
1 |
51 |
8 |
23 |
111 |
503 |
392 |
6,53 |
6,49 |
|
40 |
8 |
50 |
15 |
47 |
530 |
947 |
417 |
6,95 |
6,87 |
|
45 |
16 |
41 |
0 |
7 |
1001 |
7 |
446 |
7,43 |
7,26 |
|
50 |
1 |
15 |
9 |
15 |
75 |
555 |
480 |
8 |
8,06 |
|
55 |
9 |
43 |
18 |
30 |
583 |
1110 |
527 |
8,78 |
8,87 |
|
60 |
20 |
39 |
6 |
40 |
1239 |
400 |
601 |
10,02 |
9,9 |
|
61,58 |
5 |
20 |
16 |
7 |
320 |
967 |
647 |
10,78 |
10,49 |
|
62,5 |
|
|
|
|
|
|
|
12 |
12 |
La colonne J est la plus difficile à créer. Il s’agit d’approximer la courbe théorique delta t= F(D) par des segments de droites.
La courbe en question est obtenus en créant un diagramme après sélection des cellules A1 à A 19 et I1 à I19.
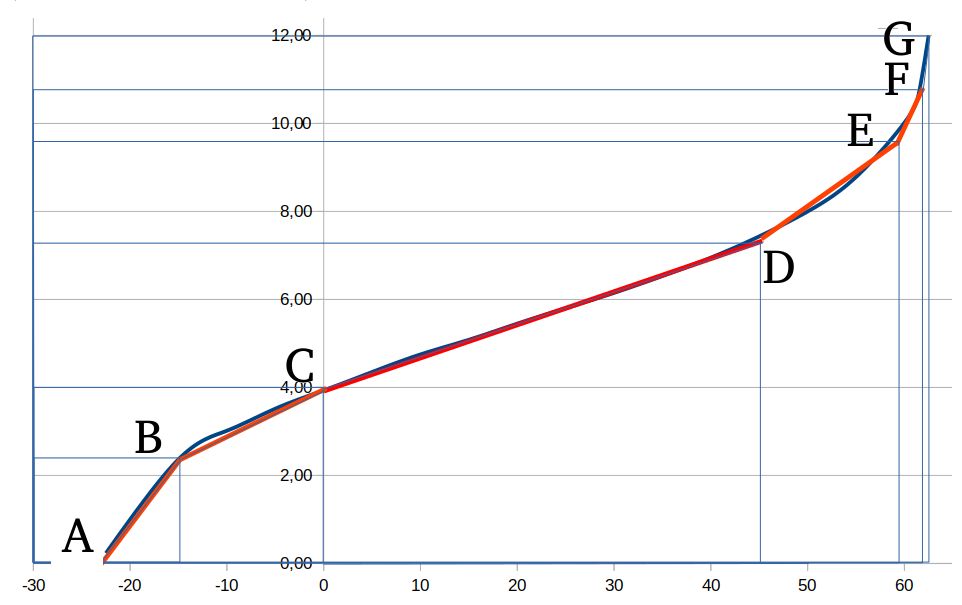
La courbe bleue sera approximée par les segments rouges.
À partir des coordonnées x, y des points A à G on établit le tableau suivant qui calcule les coefficients a et b des fonctions de type y = ax +b correspondant à chaque segment.
Rappelons que connaissant 2 points x1;y1 et x2;y2 on peut calculer a = (y2 – y1) / (x2 – x1) et b = y2 – a × x2.
| point | x | y | a | b |
|
A |
-23,07 |
0 |
|
|
|
B |
-14,97 |
2,37 |
0,29 |
6,75 |
|
C |
0,24 |
3,85 |
0,1 |
3,83 |
|
D |
44,83 |
7,26 |
0,08 |
3,83 |
|
E |
59,12 |
9,57 |
0,16 |
0,01 |
|
F |
62,24 |
10,74 |
0,38 |
-12,6 |
|
G |
62,49 |
11,94 |
4,8 |
-288,01 |
La cellule donnant a, pour le segment AB, contient =(C64-C63)/(B64-B63) sachant que la cellule marquée « Point » est en A62.
La cellule donnant b pour le segment AB contient =C64-(D64*B64).
Il ne reste plus qu’à placer la bonne formule dans la colonne J du premier tableau. Elle est un peu longue :
=SI.CONDITIONS(C3<-23,07;0;C3<-14,97;C3*0,292+6,75;C3<0,24;C3*0,1+3,82;C3<44,83;C3*0,076+3,83;C3<59,12;C3*0,161+0,013;C3<62,24;C3*0,375-12,6;C3<62,49;C3*4,8-288;C3=62,49;12;C3>62,49;12).
La formule se comprend ainsi : Si D (déclinaison) < -23,07 alors la durée d est nulle ; sinon, si D < -14,97 on est sur le segment AB et la valeur se calcule avec d = 0,29 × D + 6,75 ; sinon si D < 0,24 alors d = D × 0,1 + 3,82 ; sinon etc...
Voici le même tableau en 2 pdf.
Les période de visibilité sont inscrites en rouge si la culmination tombe pendant la nuit et en vert si elle tombe avant le début de la nuit ou après la fin.
Cette mise en évidence a été obtenue en appliquant à la plage E3:Q106 les 4 conditions suivantes:
ET(E3<=E$109;E3+$R3>E$109)
E3>E$109
ET(E3<18;E3<=E$110)
ET(E3>E$110;E3-$R3<=E$110)
La première condition examine si en ajoutant à l'heure de culmination la durée de visibilité, on dépasse le début de la nuit ( 1 heure après le coucher du soleil). On ecrit en vert.
La deuxième condition suppose que l'heure de culmination correspond à un nombre supérieure au début de la nuit. On est dans la nuit ; on écrit en rouge.
La troisième condition tient compte du fait qu'après minuit l'heure retombe à 0. On a donc des valeurs faibles et en tout état de cause inférieure à 18. La condition est vraie si on ne dépasse pas l'heure de fin de nuit. On est dans la nuit ; on écrit en rouge.
Enfin, si on dépasse l'heure de fin de nuit, la condition est vérifiée si on dépasse de moins que delta t. On ecrit en vert.
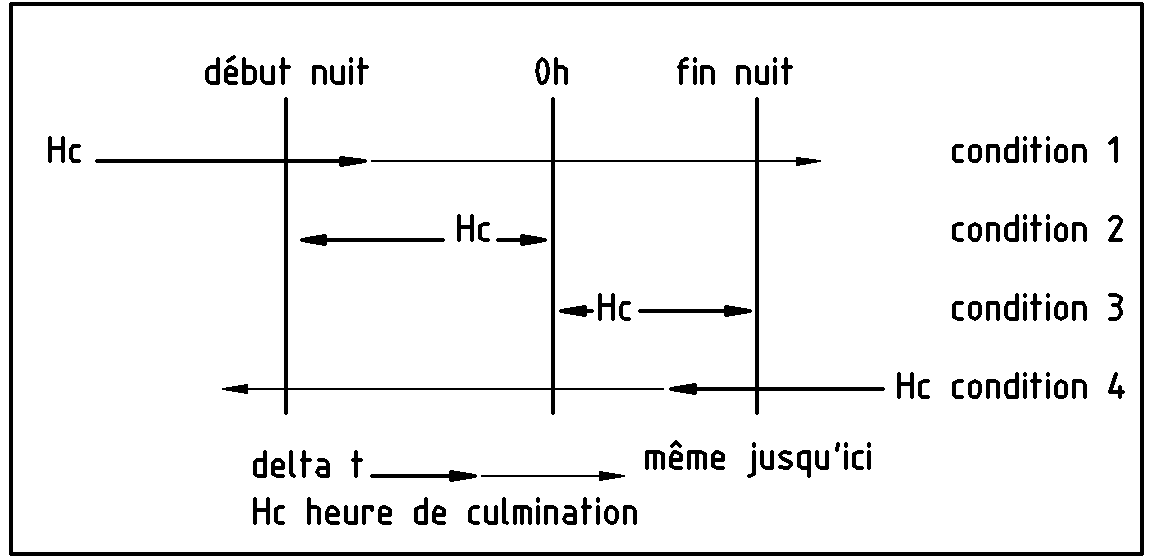
Mais j'ai décidé de griser une ligne sur 5 pour faciliter la lecture. Il a donc fallut combiner les conditions précédentes avec une fonction modulo dans une fonction ET : Soit le modulo de la ligne est nul, alors on grise, sinon on ne grise pas.
On a donc au final, 9 conditions et 5 styles :
ET(E3<=E$109;E3+$R3>E$109;MOD(LIGNE();5)>0) vert sur fond blanc
ET(E3>E$109;MOD(LIGNE();5)>0) rouge sur fond blanc
ET(E3<18;E3<=E$110;MOD(LIGNE();5)>0) rouge sur fond blanc
ET(E3>E$110;E3-$R3<=E$110;MOD(LIGNE();5)>0) vert sur fond blanc
ET(E3<=E$109;E3+$R3>E$109;MOD(LIGNE();5)=0) vert sur fond gris
ET(E3>E$109;MOD(LIGNE();5)=0) rouge sur fond gris
ET(E3<18;E3<=E$110;MOD(LIGNE();5)=0) rouge sur fond gris
ET(E3>E$110;E3-$R3<=E$110;MOD(LIGNE();5)=0) vert sur fond gris
MOD(LIGNE();5)=0 noir sur fond gris
Bon ciel!
***** © M Guignard 2022 *****

Comments powered by CComment