À quelle vitesse les étoiles défilent-elles dans le champ d’un oculaire?
À quelle vitesse les étoiles se déplacent-elles dans le ciel ? Je parle ici du déplacement apparent bien sûr. La réponse spontanée est 360° en 24h soit 15°/h ou 0,25°/min. Oui mais on sait que l’étoile polaire ne bouge pas, ou presque, donc c’est sans doute un peu plus compliqué que cela. Et pour les planètes c’est encore plus compliqué !
Cette question en appelle une autre : Quelle gamme de vitesses faut-il prévoir pour les axes d’azimut et de hauteur d’une monture azimutale ?
Je vous propose ici un tour de la question. Avant de lire cet article, lisez au besoin, ceux intitulés « comment ça tourne » et « les coordonnées équatoriales ».
NB : Pour faciliter la typographie, les angles sont notés entre chevrons. Ex l’angle <ABC>.
A -À QUELLE VITESSE DÉFILE UNE ÉTOILE DANS LE CHAMP DE L’OCULAIRE ?
On raisonne habituellement à partir de la sphère céleste, un immensément immense chapiteau de forme sphérique de rayon arbitraire mais très très très grand non par rapport à nous autres pauvres fourmis, mais par rapport à la Terre. Dans ces conditions, tous les endroits de notre planète sont très sensiblement au centre de la sphère.
Donc, je suis, vous êtes, au centre de cette sphère creuse qui tourne (en réalité qui semble tourner) sur elle-même en 23 h 56 min et une poignée de secondes, mais je dirai 24 h pour faire plus simple. L’axe de rotation passe par le centre donc par votre œil ou le pied du télescope, comme ça vous dit, et par le pôle céleste à proximité de l’étoile polaire. Cet axe est donc incliné. En fait c’est le sol ou vous êtes qui « penche ». Voir la figure ci-contre.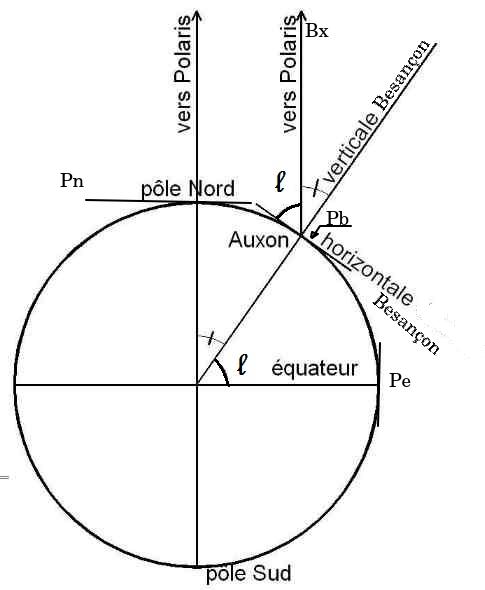
Dans un premier temps, transportons-nous pile au pôle nord. Ici, l’étoile polaire est au zénith, l’axe est vertical. Les étoiles décrivent des cercles dans des plans horizontaux. Le plus grand cercle est décrit au niveau de l’horizon. Le diamètre des cercles diminue à mesure que l’on monte. Si vous avez du mal à vous représenter cela, regardez un globe terrestre avec ses différents parallèles1. L’équateur est le plus grand et les autres diminuent à mesure que l’on monte en latitude, jusqu’à être nul au pôle.
Les étoiles que vous voyez à l’horizon sont situées sur l’équateur céleste qui est inscrit dans le même plan que l’équateur terrestre. Pour vous, ce plan est translaté au pôle nord. Rappelez-vous, le rayon de la Terre compte pour du beurre. Ces étoiles font le tour de l’horizon en 24h soit une vitesse de 0,25°/min. Une étoile met 4min pour traverser un champ de 1°. Ces étoiles décrivent un cercle dont le centre est le centre de la sphère donc vous. Ce cercle est un grand cercle de la sphère (un cercle dont le diamètre est celui de la sphère).
Certes, les autres étoiles font aussi un tour en 24h, mais ce tour est plus petit. Pour bien comprendre, prenez un globe terrestre et regardez-le comme la sphère céleste (bien que, en quelque sorte, vous soyez en train de regarder l’univers de l’extérieur). En fait vous êtes dans le globe, au centre). Prenez des gommettes et collez-les cote à cote sur tout l’équateur. Ces gommettes représentent un champ de télescope. Si vous avez placé 60 gommettes, chacune couvre un champ de 360/60 = 6° (bon, c’est plutôt le champ d’un chercheur mais peu importe). Maintenant placez des gommettes sur le parallèle de latitude 60°. Vous ne pourrez en mettre que 30. Cela signifie que le cercle à 60°de hauteur correspond à 30 champs de 6°. Ces 30 champs sont parcourus en 24h, donc chaque champ est parcourus en 24/30 = 0,8h soit 48min. 1° est parcouru en 8min.
Pour une hauteur h donnée le diamètre du cercle est celui de la sphère, multiplié par le cosinus de h. Si vous ne savez pas ce qu’est un cosinus, lisez l’encart un peu plus loin. Par exemple, à une hauteur de 45° le cosinus vaut sensiblement 0,707 donc la vitesse est également multipliée par 0,707 ce qui nous donne 10,6°/h ou 0,177°/min. Une étoile met alors environ 5,7min pour traverser un champ de 1°. À 60° de hauteur, le cosinus vaut 0,5, le champ de 1° est parcouru en 8min, c’est ce que nous avons vu plus haut.
Qu’est-ce qu’un cosinus ?
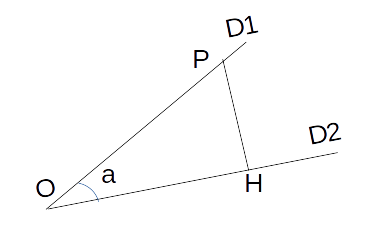 Considérez deux lignes droites D1 et D2 qui forment un angle a comme sur la figure ci-dessous. On projette un point P de D1 sur D2 en H ( c’est à dire qu’on tire une droite depuis P qui sera perpendiculaire à D2 ( l’angle OHP est droit la projection est dite orthogonale). Le rapport des longueurs OH/OP est appelé le cosinus de l’angle a. Il ne dépend pas de la distance OP mais seulement de l’angle O. Le cosinus varie entre 1 pour un angle nul et 0 pour un angle de 90°. Votre ordinateur dispose d’une calculette. En mode d’affichage scientifique, elle peut vous donner les cosinus et bien plus encore.
Considérez deux lignes droites D1 et D2 qui forment un angle a comme sur la figure ci-dessous. On projette un point P de D1 sur D2 en H ( c’est à dire qu’on tire une droite depuis P qui sera perpendiculaire à D2 ( l’angle OHP est droit la projection est dite orthogonale). Le rapport des longueurs OH/OP est appelé le cosinus de l’angle a. Il ne dépend pas de la distance OP mais seulement de l’angle O. Le cosinus varie entre 1 pour un angle nul et 0 pour un angle de 90°. Votre ordinateur dispose d’une calculette. En mode d’affichage scientifique, elle peut vous donner les cosinus et bien plus encore.
On rencontre souvent les cosinus en maths et en physique. Par exemple, si vous tractez un bateau avec une corde, depuis la berge, si F est la force de traction, et a l’angle entre la direction de la corde et la direction du bateau alors la composante utile de la force vaut F × cos(a). Autre exemple : Si la normale à un panneau photovoltaïque fait un angle a avec la direction du soleil, il ne récupère que cos(a) fois la quantité de lumière disponible. La normale est la droite perpendiculaire au plan considéré.
Les astronomes graduent la sphère céleste de la même façon que les géographes graduent la terre (voir ici). Donc pour les esquimaux, la hauteur d’une étoile est égale à sa déclinaison.
Revenez maintenant en France. L’axe de rotation de la sphère céleste a basculé d’environ 45°, les cercles décrits par les étoiles ont basculés d’autant. L’équateur céleste est incliné par rapport à la verticale, de la latitude du lieu. Vous pouvez en repérer 3 points très facilement : Le point d’horizon Est, le point d’horizon Ouest et le point d’azimut Sud à une hauteur égale au complément de la latitude (ce qu’il faut ajouter à la latitude pour faire 90°). Bien sûr toutes nos graduations en déclinaison ont basculé d’autant. Chez moi, la latitude L, est proche de 47°, le point sud de l’équateur céleste est à
90 - 47 = 43°.
Dans le plan méridien 2, une étoile de déclinaison D, est à une hauteur
hs = 43° + D°
en comptant depuis l’horizon sud. Si l’étoile est dans la moitié Nord (coté Nord d’un mur infini orienté Est-Ouest) la hauteur est égale au supplément de hs soit
h° = 180 - (L + D).
Les étoiles à moins de 43° (coté sud et toujours sur le méridien) sont dans l’hémisphère céleste sud, partiellement invisible sous nos latitudes.
Certaines étoiles décrivent un cercle complet sans jamais passer sous l’horizon, elles sont dites circumpolaires. Ces étoiles coupent donc le plan méridien en un 2e point plus bas. Pour D = L, le cercle est tangent au sol, le point le plus haut est au zénith. Une étoile est circumpolaire si D ≥ L. La hauteur h2, du 2e point est donné par la formule
h2° = L -90 + D.
Les vitesses de déplacement du champ d’observation sont les mêmes qu’au pôle nord, à condition de se référer aux déclinaisons. Une étoile à la déclinaison D = 0° se déplacera dans le champ de votre télescope à 0,25°/min, comme au pôle nord mais sur un cercle incliné par rapport au sol. Une étoile à la déclinaison D = 60° se déplacera deux fois moins vite.
B -La vitesse de variation de la hauteur (Vh)
Quelle gamme de vitesse faut-il prévoir pour motoriser en hauteur une monture azimutale ? Disons tout de suite que dans le cas général le calcul n’est pas du tout simple. Voyez un peu l’équation qui nous donne la hauteur :
sin(h) = sin(L)*sin(D) + cos(L) *cos(D)*cos(H) (1)
où h est la hauteur de l’étoile ; L la latitude du lieu ; D la déclinaison de l’étoile et H l’angle horaire. L’angle horaire vaut 0 au méridien, 18h (ou -90°) à l’horizon Est et 6h (ou 90°) à l’horizon Ouest.
Remarquez que cela ne nous donne par directement la hauteur mais son sinus.
La valeur de h dépend donc de 3 données. Pour un endroit de la Terre fixé, sin(L) et cos(L) sont constants, il reste deux variables : D et H.
Commençons simplement. Au passage dans le plan méridien, les tangentes de tous les cercles sont horizontales, donc la vitesse Vh est nulle, mais pendant un temps mathématiquement infiniment bref.
À partir d’ici, je vais me placer à une latitude de 45°, cela facilitera les explications et les calculs et l’écart reste modeste partout en France.
Plaçons-nous sur l’équateur céleste, à l’horizon Est. La tangente est située dans un plan vertical, elle est inclinée de 45° par rapport à la verticale. Les composantes horizontales et verticales sont égales. Dans un triangle rectangle isocèle, les côtés de l’angle droit ont pour longueur l’hypoténuse divisée par √2 . Pour nous l’hypoténuse vaut 15°/h, donc la vitesse de la hauteur est de 15 / √2 = 10,6° /h soit 0,177°/min. Le plan vertical contenant la tangente à l’équateur à l’horizon Est, est perpendiculaire à la direction dans laquelle on le regarde, on le voit donc en vraie grandeur. Notre valeur de 0,177°/min est correcte, elle est √2 fois plus faible qu’à l’équateur (terrestre) où la tangente monte verticalement.
Une autre façon d’aborder le calcul consiste à partir de la formule (1):
sin(h) = sin(L)*sin(D) + cos(L) *cos(D)*cos(H)
Pour une latitude de 45°, sin(L)=cos(L)= 1/√2 que je remplacerai par 0,707. La formule (1) devient alors :
sin(h) = 0,707 ( sin(D) + Cos(D)*cos(H) (2)
et à l’équateur D = 0 ; sin(D) = 0 ; cos(D) = 1 donc on a :
sin(h) = 0,707 * cos(H) (3)
Ce qui peut s’écrire :
sin(h) = 0,707 * sin(H1) (4)
où H1 = H + 90°.
À l’horizon, pour D=0, H = -90° donc H1=0 et sin(h) = 0.
Pour les petits angles, les sinus sont sensiblement égaux aux angles, donc
h = 0,707H1.
Donc la vitesse de h est 0,707 fois celle de H.
Pour une déclinaison quelconque et H quelconque, il faut reprendre la formule (2)
Une façon de traiter le problème dans son ensemble sans trop se faire chauffer les neurones, consiste à utiliser un tableur tel que Calc de LibreOffice ou Excel de la suite Microsoft pour ceux qui préfèrent payer. On se réserve une cellule (G2) pour inscrire la déclinaison. On obtient une série de vitesses pour les différentes valeurs de H et l’indication de la plus forte en H4. Il suffit de changer la déclinaison (en radiants) pour disposer immédiatement d’une nouvelle série de vitesses.
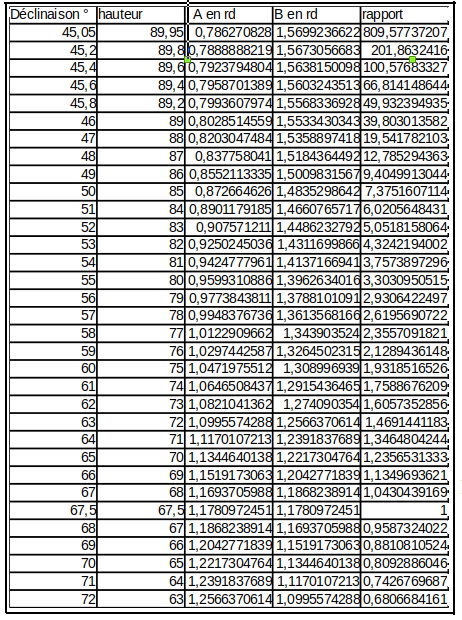
La figure suivante est un extrait du tableau
NB : Pour une déclinaison de 45° (Π / 4), sous une latitude de 45° le cercle de déclinaison 45° est tangent au sol au Nord.
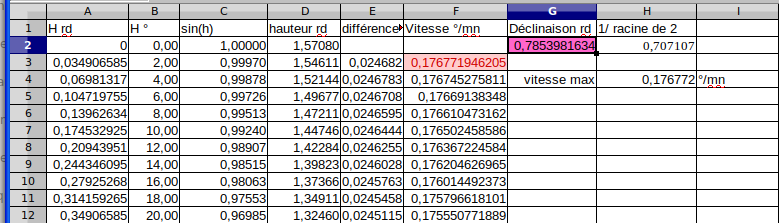
Voici le même tableau avec affichage des formules :

La colonne B donne les valeurs de H de 2 en 2 degrés. La colonne A, reprend les mêmes valeurs en radians pour faciliter les calculs. La colonne C calcule le sinus de la hauteur. La colonne D donne la hauteur en radians. En E on a la différence de 2 hauteurs consécutives. Enfin, la colonne F calcule les vitesses en °/min.
La cellule G2 contient la valeur de la déclinaison en radians (ici π/4). La cellule H4 indique le maximum des vitesses calculées.
Un formatage conditionnel appliqué aux cellules F3 à F93 permet de faire ressortir le maximum.
Avec un tableau identique, vous pourrez facilement vous faire une idée précise de la façon dont varie la vitesse en hauteur dans tous les cas de figure. Rien ne vous empêche de compliquer légèrement les formules pour les adapter à votre latitude exacte.
N’oubliez pas que les hauteurs négatives correspondent à des étoiles non visibles !
C -Comment varie l’azimut ?
Bien que plus facile à expliquer, les variations d’azimut au cours du temps réservent quelques surprises au néophyte.
Rendons-nous à nouveau au pôle nord. Les étoiles décrivent des cercles horizontaux. Les étoiles qui sont au raz de l’horizon font un tour en 24h, elles sont vue en face, leur vitesse est donc de 0,25°/min.
Toutes les étoiles dans un même plan vertical sont au même azimut et tournent donc comme leur sœur qui est au raz de l’horizon donc à la même vitesse de 1° en 4min.
Prenons l’avion pour l’équateur. Rappelez-vous, les cercles décrits par les étoiles sont verticaux. Considérons le cercle de déclinaison nulle, orienté Est-Ouest et suivons une étoile depuis son lever à l’Est. L’étoile monte dans le ciel sans changer d’azimut. La vitesse azimutale est donc nulle (première surprise). Mais quand on atteint le zénith Z, on passe brusquement de l’azimut Est à l’azimut Ouest. La vitesse est donc infinie pendant un temps infiniment court (deuxième surprise) ! Puis elle retombe à 0 pour les 6 prochaines heures. On voit que le zénith est un point très particulier.
Revenons en France. Le passage au zénith se passe presque de la même façon : On est sur le cercle de déclinaison L. On s’approche progressivement de l’azimut Est à mesure qu’on monte sur le cercle de déclinaison égale à la latitude. L’azimut Est, est atteint à Z - ε; à Z + ε on est à l’azimut Ouest.
Est-ce à dire que le moteur d’azimut d’une monture doit être capable de vitesse folles ? Assurément non. D’abord, vous pouvez purement et simplement éviter le zénith d’ailleurs inatteignable par certaines montures. Ensuite, vous disposez d’un certain champ donc d’une certaine durée pour vous retourner. En réalité, c’est votre patience qui décidera de la vitesse nécessaire. Combien de temps jugez-vous acceptable d’attendre pour faire un demi-tour ?
Reste à satisfaire une curiosité intellectuelle : Comment se fait-il que l’azimut puisse varier plus vite que la rotation du ciel ?
Considérons une étoile de déclinaison 0 passant au méridien. Soit :
-
S1 sa position un peu avant qu’elle ne passe au sud à une hauteur
h = 90°- L,
-
S2 sa position un peu après le franchissement du sud.
-
P1 la projection sur le plan du sol de S1 et P2 celle de S2.
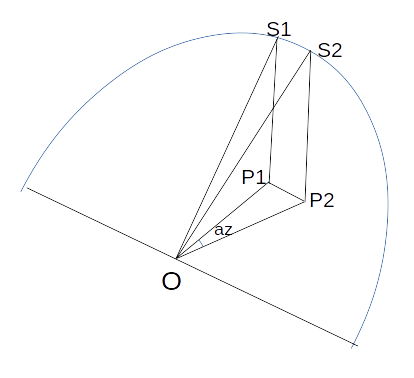
L’arc S1S2 étant petit, on peut écrire
tg(<S1OS2>) = S1S2 / R
où R est le rayon de la sphère céleste.
et tg(az) = P1P2 / OP1
mais d’une part, P1P2 = S1S2
et d’autre part
OP1 = R*cos(<S1OP1>)= R * cos(h)
OP1 = R * cos (45°)
donc tg(az) = tg(<S1OS2>) / cos(45°
tg(az) = tg( <S1OS2>) * √2
et comme les angles sont petits
az = <S1OS2> * √2
Ainsi, l’azimut évolue √2 fois plus vite que l’étoile avance sur sa trajectoire.
Quand on monte dans le ciel en changeant de déclinaison, cos(h) diminue mais en même temps cos(D) diminue aussi. La question est : Qui est ce qui l’emporte ?
Restons sous une latitude de 45° et montons de 10°, soit à D = 10°. Cos(D) = 0,98 n’a guère changé, par contre cos(55°) = 0,57. Finalement on a gagné un facteur 1,20.
Montons carrément a D = 45°. On est au zénith et on connaît la réponse mais vérifions.
On a a = 1° * cos(45°) / cos(90°)
On divise par 0 ce qui nous donne l’infini.
Continuons à augmenter D au-delà de 45°. cos(D) diminue, la hauteur diminue, tout va dans le même sens pour réduire a. Un tableau Calc me permet de voir que le coefficient cos(D) / cos(h) infini à 90° de hauteur, tombe à moins de 202 à 89,8° et à moins de 20 à 88° et atteint 1 pour D = 67,5°.
Supposons que notre monture soit capable de faire un tour en 5min. Il y a 1440min dans un jour. Notre monture tourne 1440 / 5 = 288 fois plus vite que la Terre. On pourra donc suivre sans problème une étoile qui passerait quasiment à raz du zénith.
Pour clore la question voici une carte qui donne les différentes vitesses de variation de l'azimut pour une moitié de ciel visible, l'autre moitié étant symétrique.
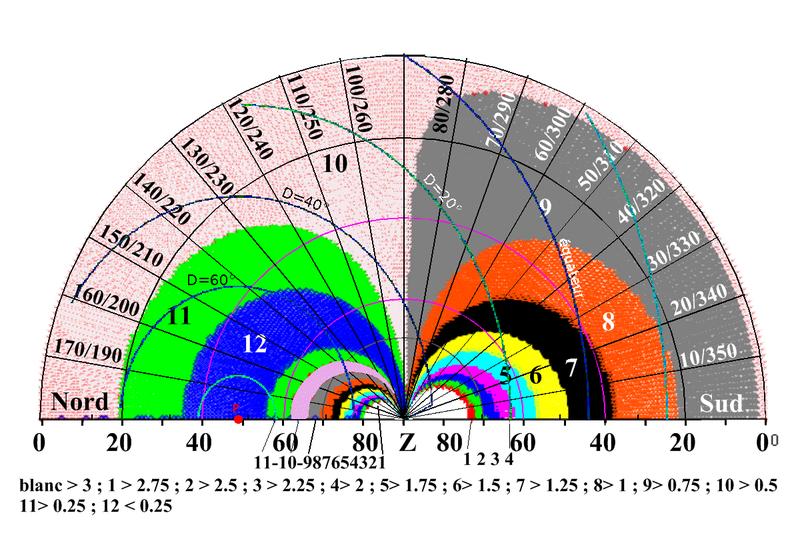
Chaque couleur correspond à une gamme de vitesse. Voir les numéros inscrit en bas pour les zones étroites et à l'intérieure des zones larges. Les droites marquent les points de même azimut; les demi cercles centrés sur le point Z repèrent les points de même hauteur. Les arcs repérés D= xx montrent les points de même déclinaison. Le gros point rouge montre le pôle nord céleste. Cette carte est valable pour les environs de Besançon.
****** © M Guignard ******
1Notez que parallèle est ici masculin, parce que l’on parle de cercles parallèles, alors qu’habituellement on dit une parallèle pour une droite parallèle
2Pour vous représenter le plan méridien, imaginez un mur très très haut courant du nord au sud sur des km en passant par votre lieu d’observation.